
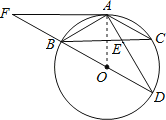
【题目】如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4,

(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
【答案】(1)见解析;(2)AB=![]() .(3)直线FA与⊙O相切.
.(3)直线FA与⊙O相切.
【解析】
试题分析:(1)根据AB=AC,可得∠ABC=∠C,利用等量代换可得∠ABC=∠D然后即可证明△ABE∽△ADB.
(2)根据△ABE∽△ADB,利用其对应边成比例,将已知数值代入即可求得AB的长.
(3)连接OA,根据BD为⊙O的直径可得∠BAD=90°,利用勾股定理求得BD,然后再求证∠OAF=90°即可.
(1)证明:∵AB=AC,
∴∠ABC=∠C(等边对等角),
∵∠C=∠D(同弧所对的圆周角相等),
∴∠ABC=∠D(等量代换),
又∵∠BAE=∠DAB,
∴△ABE∽△ADB,
(2)解:∵△ABE∽△ADB,
∴![]() ,
,
∴AB2=ADAE=(AE+ED)AE=(2+4)×2=12,
∴AB=![]() .
.
(3)解:直线FA与⊙O相切,理由如下:
连接OA,∵BD为⊙O的直径,
∴∠BAD=90°,
∴![]() =4
=4![]()
BF=BO=![]() ,
,
∵AB=![]() ,
,
∴BF=BO=AB,
∴∠OAF=90°,
∴OA⊥AF,
∵AO是圆的半径,
∴直线FA与⊙O相切.


科目:初中数学 来源: 题型:
【题目】若多项式﹣6ab+18abc+24ab2的一个因式是﹣6ab,则其余的因式是( )
A. 1﹣3c﹣4b B. ﹣1﹣3c+4b C. 1+3c﹣4b D. ﹣1﹣3c﹣4b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方成同学看到一则材料:甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地.设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示.
方成思考后发现了如图1的部分正确信息:乙先出发1h;甲出发0.5小时与乙相遇.
请你帮助方成同学解决以下问题:
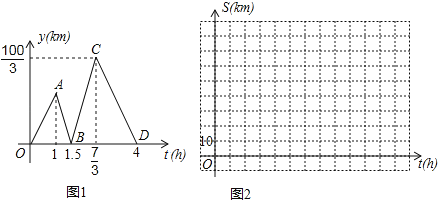
(1)分别求出线段BC,CD所在直线的函数表达式;
(2)当20<y<30时,求t的取值范围;
(3)分别求出甲,乙行驶的路程S甲,S乙与时间t的函数表达式,并在图2所给的直角坐标系中分别画出它们的图象;
(4)丙骑摩托车与乙同时出发,从N地沿同一公路匀速前往M地,若丙经过![]() h与乙相遇,问丙出发后多少时间与甲相遇?
h与乙相遇,问丙出发后多少时间与甲相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,以△ABC中的AB、AC为边分别向外作正方形ADEB、ACGF,
连接DC、BF。(相关知识链接:正方形的四条边都相等,四个角都是直角)
(1)观察图形,利用旋转的观点说明:
△ADC绕着点__ ___逆时针旋转___ __°得到△ABF。
(2)猜想:CD与BF有怎样的数量关系和位置关系?并证明你的猜想.
(3)若CD与BF相交于点M,求∠AMF的度数。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列选项中,具有相反意义的量是( )
A.收入20元与支出30元
B.上升了6米和后退了7米
C.卖出10斤米和盈利10元
D.向东行30米和向北行30米
查看答案和解析>>
科目:初中数学 来源: 题型:
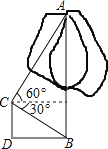
【题目】为申办2013年冬奥会,须改变某城市的交通状况,在街道拓宽工程中,要伐掉一棵树AB,在地面上事先划定以B为圆心,半径与AB等长的圆形危险区.现在某工人站在离B点3米远的D处,从C点测得树的顶端A点的仰角为60°,树的底部B点的俯角为30°.问:距离B点8米元的保护物是否存在危险?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com