
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,
的中点,![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .
.

(1)如图1,![]() 与
与![]() 的数量关系是__________.
的数量关系是__________.
(2)如图2,若![]() 是线段
是线段![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 、
、![]() 重合),连接
重合),连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,请猜想
,请猜想![]() 三者之间的数量关系,并证明你的结论;
三者之间的数量关系,并证明你的结论;
【答案】(1)DE=![]() BC;(2)
BC;(2)![]()
【解析】
(1)由∠ACB=90°,∠A=30°得到∠B=60°,根据直角三角形斜边上中线性质得到DB=DC,则可判断△DCB为等边三角形,由于DE⊥BC,可得DE=![]() BD=
BD=![]() BC;
BC;
(2)根据旋转的性质得到∠PDF=60°,DP=DF,易得∠CDP=∠BDF,则可根据“SAS”判断△DCP≌△DBF,则CP=BF,利用CP+BP =BC,DE=![]() BC可得到DE =
BC可得到DE =![]() (BF+BP).
(BF+BP).
解:(1)∵∠ACB=90°,∠A=30°,
∴∠B=60°,
∵点D是AB的中点,
∴DB=DC,
∴△DCB为等边三角形,
∵DE⊥BC,
∴DE=![]() BC;
BC;
故答案为DE=![]() BD=
BD=![]() BC.
BC.
(2)DE =![]() (BF+BP).理由如下:
(BF+BP).理由如下:
∵线段DP绕点D逆时针旋转60°,得到线段DF,
∴∠PDF=60°,DP=DF,
而∠CDB=60°,
∴∠CDB-∠PDB=∠PDF-∠PDB,
∴∠CDP=∠BDF,
在△DCP和△DBF中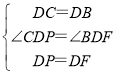 ,
,
∴△DCP≌△DBF(SAS),
∴CP=BF,
而CP=BC-BP,
∴BF+BP=BC,
∵DE=![]() BC,
BC,
∴DE =![]() (BF+BP);
(BF+BP);
故答案为DE =![]() (BF+BP).
(BF+BP).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】近年来,随着电子商务的快速发展,电商包裹件总量占当年快递件总量的比例逐年增长.根据某快递公司某网点的数据统计,得到如下统计表:

(1)直接写出m,n的值,并在图中画出电商包裹件总量占快递件总量百分比的折线统计图;
(2)若2019年该网点快递件总量预计达到7万件,请根据图表信息,估计2019年电商包裹件总量约为多少万件?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣2mx+m2+m﹣1(m是常数)的顶点为P,直线![]() :y=x﹣1
:y=x﹣1
(1)求证:点P在直线![]() 上;
上;
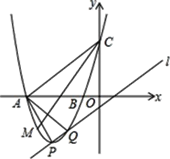
(2)当m=﹣3时,抛物线与x轴交于A,B两点,与y轴交于点C,与直线![]() 的另一个交点为Q,M是x轴下方抛物线上的一点,∠ACM=∠PAQ(如图),求点M的坐标;
的另一个交点为Q,M是x轴下方抛物线上的一点,∠ACM=∠PAQ(如图),求点M的坐标;
(3)若以抛物线和直线![]() 的两个交点及坐标原点为顶点的三角形是等腰三角形,请直接写出所有符合条件的m的值.
的两个交点及坐标原点为顶点的三角形是等腰三角形,请直接写出所有符合条件的m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
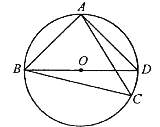
【题目】如图,![]() 为
为![]() 的外接圆上的一动点(点
的外接圆上的一动点(点![]() 不在
不在![]() 上,且不与点
上,且不与点![]() 、
、![]() 重合),
重合),![]() .
.
(1)求证:![]() 是该外接圆的直径;
是该外接圆的直径;
(2)连接![]() ,求证:涯
,求证:涯![]() ;
;
(3)若![]() 关于直线
关于直线![]() 的对称图形为
的对称图形为![]() ,连接
,连接![]() ,试探究
,试探究![]() 、
、![]() 、
、![]() 三者之间满足的等量关系,并证明你的结论.
三者之间满足的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
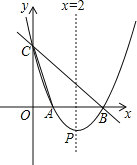
【题目】如图,直线y=﹣x+3与x轴,y轴分别相交于点B,C,经过B,C两点的抛物线y=ax2+bx+c与x轴的另一交点为A,顶点为P,且对称轴是直线x=2.
(1)求该抛物线的函数表达式;
(2)请问在抛物线上是否存在点Q,使得以点B,C,Q为顶点的三角形为直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由;
(3)过S(0,4)的动直线l交抛物线于M,N两点,试问抛物线上是否存在定点T,使得不过定点T的任意直线l都有∠MTN=90°?若存在,请求出点T的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中发现:从零时起,井内空气中CO的浓度达到4 mg/L,此后浓度呈直线型增加,在第7小时达到最高值46 mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降,如图,根据题中相关信息回答下列问题:
(1)求爆炸前后空气中CO浓度y与时间x的函数关系式,并写出相应的自变量取值范围;
(2)当空气中的CO浓度达到34 mg/L时,井下3 km的矿工接到自动报警信号,这时他们至少要以多少km/h的速度撤离才能在爆炸前逃生?
(3)矿工只有在空气中的CO浓度降到4 mg/L及以下时,才能回到矿井开展生产自救,求矿工至少在爆炸后多少小时才能下井?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校长暑假将带领该校前级“三好学生”去北京大学游学,甲旅行社说:如果校长买全票一 张,则其余的学生可享受半价优惠.乙旅行社说:“包括校长在内全部按票价的六折优惠”. 若全票价为![]() 元,两家旅行社的服务质量相同,根据三好学生的人数你认为选择哪一 家旅行社才会比较合算?
元,两家旅行社的服务质量相同,根据三好学生的人数你认为选择哪一 家旅行社才会比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分别直方图和扇形统计图:

根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图
(2)求扇形统计图中m的值和E组对应的圆心角度数
(3)请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com