练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．如图，下面每个图形中的四个数都是按相同的规律填写的，根据此规律确定x的值为370．

    分析 首先观察规律，求得n与m的值，再由右下角数字第n个的规律：2n（2n-1）-n，求得答案．

    解答 解：∵左下角数字为偶数，右上角数字为奇数，
    ∴2n=20，m=2n-1，
    解得：n=10，m=19，
    ∵右下角数字：第一个：1=1×2-1，
    第二个：10=3×4-2，
    第三个：27=5×6-3，
    ∴第n个：2n（2n-1）-n，
    ∴x=19×20-10=370．
    故答案为：370．

    点评 此题考查了数字规律性问题．注意首先求得n与m的值是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    16．若点P（a，b）在第一象限，则点P1（-a，-b）在（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．先化简，再求值：$\frac{x-3}{3{x}^{2}-6x}$÷（x+2-$\frac{5}{x-2}$），然后从-$\sqrt{2}＜x≤3$中选一个合格的整数作为x的值代入求值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．某校九年级（1）班全体学生2016年初中毕业体育考试的成绩统计如表：
    成绩（分）35394244454850
    人数（人）2566876
    根据表中的信息判断，下列结论中错误的是（　　）
    A．该班一共有40名同学
    B．该班学生这次考试成绩的众数是45分
    C．该班学生这次考试成绩的中位数是45分
    D．该班学生这次考试成绩的平均数是45分

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

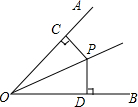    1．如图，OP为∠AOB的角平分线，PC⊥OA，PD⊥OB，垂足分别是C、D，则下列结论错误的是（　　）
    A．PC=PDB．∠CPD=∠DOPC．∠CPO=∠DPOD．OC=OD

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

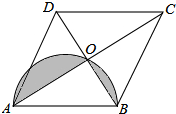    11．如图，菱形ABCD的对角线相交于点O，AC=8，BD=6，以AB为直径作一个半圆，则图中阴影部分的面积为$\frac{25}{8}$π-6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．运行程序如图所示，规定：从“输入一个值x”到“结果是否＞95”为一次程序操作，如果程序操作进行了三次才停止，那么x的取值范围是（　　）
    A．x≥11B．11≤x＜23C．11＜x≤23D．x≤23

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．已知n边形的内角和θ=（n-2）×180°．
    （1）甲同学说，θ能取360°；而乙同学说，θ也能取630°．甲、乙的说法对吗？若对，求出边数n．若不对，说明理由；
    （2）若n边形变为（n+x）边形，发现内角和增加了360°，用列方程的方法确定x．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．在等边△ABC中，

    （1）如图1，P，Q是BC边上的两点，AP=AQ，∠BAP=20°，求∠AQB的度数；
    （2）点P，Q是BC边上的两个动点（不与点B，C重合），点P在点Q的左侧，且AP=AQ，点Q关于直线AC的对称点为M，连接AM，PM．
    ①依题意将图2补全；
    ②小茹通过观察、实验提出猜想：在点P，Q运动的过程中，始终有PA=PM，小茹把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：
    想法1：要证明PA=PM，只需证△APM是等边三角形；
    想法2：在BA上取一点N，使得BN=BP，要证明PA=PM，只需证△ANP≌△PCM；
    想法3：将线段BP绕点B顺时针旋转60°，得到线段BK，要证PA=PM，只需证PA=CK，PM=CK…
    请你参考上面的想法，帮助小茹证明PA=PM（一种方法即可）．

    查看答案和解析>>

    同步练习册答案