

���� ��1��ֻ���������E�����꣬Ȼ�����ô���ϵ�����Ϳɽ�����⣻
��2������F��PN��x����N����EB��M����ͼ1�����F�ĺ�����Ϊm���Ϳ��ú�m�Ĵ���ʽ��ʾ��FM�ij���������ʾ����EFB�������Ȼ�����ö��κ�������ֵ�ԾͿɽ�����⣻
��3�����������C��G�����꣬Ȼ�����AG��GC��AC�����ݹ��ɶ������涨���ɵõ���AGC=90�㣬Ȼ���������Ǻ����Ķ������tan��GAC���ɡ�BAP=��GAC�ɵõ�tan��BAP����ֱ��AP��y��Ľ���ΪQ����Rt��AOQ���������Ǻ��������OQ���Ӷ��õ���Q�����꣬�������ֱ��OQ�Ľ���ʽ��Ȼ��ͨ���ⷽ���飬�Ϳ������P�����꣮
��� �⣺��1����B��3��0����EO=BO��
��EO=BO=3��E��0��-3����
�ߵ�B��E��������y=ax2-2ax+c�ϣ�
��$\left\{\begin{array}{l}{9a-6a+c=0}\\{c=-3}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=1}\\{c=-3}\end{array}\right.$��
�������ߵĽ���ʽΪy=x2-2x-3��
��ֱ��EB�Ľ���ʽΪy=kx+b��
����$\left\{\begin{array}{l}{3k+b=0}\\{b=-3}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=1}\\{b=-3}\end{array}\right.$��
��ֱ��EB�Ľ���ʽΪy=x-3��
��2������F��PN��x����N����EB��M����ͼ1��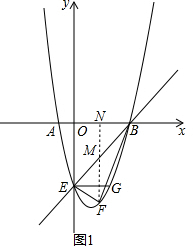
���F�ĺ�����Ϊm������
yF=m2-2m-3��yM=m-3��
��MF=��m-3��-��m2-2m-3��=-m2+3m��
��S��EFB=S��EFM+S��BFM
=$\frac{1}{2}$MF•ON+$\frac{1}{2}$MF•BN
=$\frac{1}{2}$OB•MF
=$\frac{1}{2}$��3����-m2+3m��
=-$\frac{3}{2}$��m-$\frac{3}{2}$��2+$\frac{27}{8}$��
��-$\frac{3}{2}$��0��
�൱m=$\frac{3}{2}$ʱ��S��EFBȡ�����ֵ�����ֵΪ$\frac{27}{8}$��
��ʱyP=��$\frac{3}{2}$��2-2��$\frac{3}{2}$-3=-$\frac{15}{4}$��
���P��������$\frac{3}{2}$��-$\frac{15}{4}$����
��3������GC��
��y=x2-2x-3=��x-1��2-4��
�ɵö���C��1��-4�����Գ���Ϊx=1��
��y=0ʱ��x2-2x-3=0��
���x1=-1��x2=3��
���A��������-1��0����
��EG��x�ᣬE��0��-3����
�ɵ�E��G���ڶԳ���x=1�Գƣ�
����G��2��-3����
��������֮��ľ��빫ʽ�ɵ�
AG=$\sqrt{��2+1��^{2}+��-3-0��^{2}}$=3$\sqrt{2}$��
AC=$\sqrt{��1+1��^{2}+��-4-0��^{2}}$=2$\sqrt{5}$��
GC=$\sqrt{��1-2��^{2}+��-4+3��^{2}}$=$\sqrt{2}$��
��AG2+GC2=AC2��
���AGC=90�㣬
��tan��GAC=$\frac{GC}{AG}$=$\frac{\sqrt{2}}{3\sqrt{2}}$=$\frac{1}{3}$��
�ߡ�BAP=��GAC��
��tan��BAP=$\frac{1}{3}$��
��ֱ��AP��y�ύ�ڵ�Q��
��Rt��AOQ��tan��BAP=$\frac{OQ}{OA}$=$\frac{OQ}{1}$=$\frac{1}{3}$��
��OQ=$\frac{1}{3}$��
���Q��������0��$\frac{1}{3}$����0��-$\frac{1}{3}$����
�ٵ���Q������Ϊ��0��$\frac{1}{3}$��ʱ����ͼ2�٣�
��A��-1��0����Q��0��$\frac{1}{3}$���ɵ�ֱ��AP�Ľ���ʽΪy=$\frac{1}{3}$x+$\frac{1}{3}$��
�ⷽ����$\left\{\begin{array}{l}{y=\frac{1}{3}x+\frac{1}{3}}\\{y={x}^{2}-2x-3}\end{array}\right.$����
$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{y}_{1}=0}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{2}=\frac{10}{3}}\\{{y}_{2}=\frac{13}{9}}\end{array}\right.$��
���P��������$\frac{10}{3}$��$\frac{13}{9}$����
�ڵ���Q������Ϊ��0��-$\frac{1}{3}$��ʱ����ͼ2�ڣ�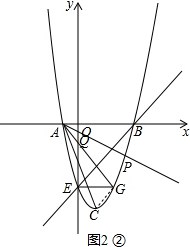
��A��-1��0����Q��0��-$\frac{1}{3}$���ɵ�ֱ��AP�Ľ���ʽΪy=-$\frac{1}{3}$x-$\frac{1}{3}$��
�ⷽ����$\left\{\begin{array}{l}{y=-\frac{1}{3}x-\frac{1}{3}}\\{y={x}^{2}-2x-3}\end{array}\right.$����
$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{y}_{1}=0}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{2}=\frac{8}{3}}\\{{y}_{2}=-\frac{11}{9}}\end{array}\right.$
���P��������$\frac{8}{3}$��-$\frac{11}{9}$����
������������P��������$\frac{10}{3}$��$\frac{13}{9}$����$\frac{8}{3}$��-$\frac{11}{9}$����
���� ������Ҫ�����˶��κ�������Գ��ԡ���ֵ�ԡ����ô���ϵ������������ֱ�ߵĽ���ʽ�����Ǻ����Ķ��塢���ɶ������涨������һԪ���η��̡���ֱ���������ߵĽ��㡢����֮��ľ��빫ʽ��֪ʶ���ۺ��ԱȽ�ǿ���ڽ������Ĺ����У��õ��˷������ۡ�����ϵ�������䷽�����������Ҫ����ѧ˼�뷽����Ӧ�������գ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����Ϊԭ����10�� | B�� | ��ʽ��ֵ���� | ||
| C�� | ��СΪԭ����$\frac{1}{10}$ | D�� | ��СΪԭ����$\frac{1}{100}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����ƽ��2����λ | B�� | ����ƽ��2����λ | C�� | ����ƽ��6����λ | D�� | ����ƽ��6����λ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵxOy�У�������y=ax2+bx+c��x���ڵ�A��B����y���ڵ�M��OA=3��tan��AMO=$\frac{3}{4}$��OM=OB��
��ͼ����ƽ��ֱ������ϵxOy�У�������y=ax2+bx+c��x���ڵ�A��B����y���ڵ�M��OA=3��tan��AMO=$\frac{3}{4}$��OM=OB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
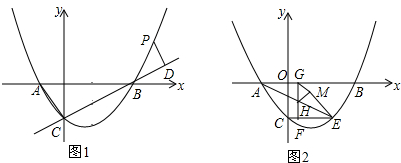
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �ڵ�����ABC�У����ǡ�A=100�㣬����B��ƽ���߽�AC�ڵ�E����֤��AE+BE=BC��
�ڵ�����ABC�У����ǡ�A=100�㣬����B��ƽ���߽�AC�ڵ�E����֤��AE+BE=BC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����ͼ | B�� | ����ͼ | C�� | ����ͼ | D�� | ֱ��ͼ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com