
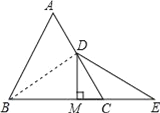
【题目】如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M.
(1)求∠E的度数.
(2)求证:M是BE的中点.

【答案】(1)∠E=30°;(2)证明见解析.
【解析】试题分析:(1)由等边△ABC的性质可得:∠ACB=∠ABC=60°,然后根据等边对等角可得:∠E=∠CDE,最后根据外角的性质可求∠E的度数;
(2)连接BD,由等边三角形的三线合一的性质可得:∠DBC=![]() ∠ABC=
∠ABC=![]() ×60°=30°,结合(1)的结论可得:∠DBC=∠E,然后根据等角对等边,可得:DB=DE,最后根据等腰三角形的三线合一的性质可得:M是BE的中点.
×60°=30°,结合(1)的结论可得:∠DBC=∠E,然后根据等角对等边,可得:DB=DE,最后根据等腰三角形的三线合一的性质可得:M是BE的中点.
试题解析:(1)∵三角形ABC是等边△ABC,
∴∠ACB=∠ABC=60°,
又∵CE=CD,
∴∠E=∠CDE,
又∵∠ACB=∠E+∠CDE,
∴∠E=![]() ∠ACB=30°;
∠ACB=30°;
(2)连接BD,
∵等边△ABC中,D是AC的中点,
∴∠DBC=![]() ∠ABC=
∠ABC=![]() ×60°=30°
×60°=30°
由(1)知∠E=30°
∴∠DBC=∠E=30°
∴DB=DE
又∵DM⊥BC
∴M是BE的中点.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】(1)如图①,OP是∠MON的平分线,点A为OM上一点,点B为OP上一点.请你利用该图形在ON上找一点C,使△COB≌△AOB,请在图①画出图形.参考这个作全等三角形的方法,解答下列问题:
(2)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你写出FE与FD之间的数量关系,并说明理由;
(3)如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其他条件不变,在(2)中所得结论是否仍然成立?请你直接作出判断,不必说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着柴静纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同.
(1)求一台A型空气净化器和一台B型空气净化器的进价各为多少元?
(2)在销售过程中,A型空气净化器因为净化能力强,噪音小而更受消费者的欢迎.为了增大B型空气净化器的销量,商社电器决定对B型空气净化器进行降价销售,经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商社电器销售B型空气净化器的利润为3200元,请问商社电器应将B型空气净化器的售价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB为⊙ O的直径,点C、D在⊙ O上,且BC=6cm,AC=8cm,∠ABD=45°.
(1)求弧BD的长;
(2)求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①如果两条直线都与第三条直线平行,那么这两条直线也互相平行;②内错角相等;③在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行;④相等的角是对顶角. 其中,真命题有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com