
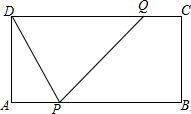
 在长方形ABCD中,AB=16cm,BC=6cm,点P从A点开始沿AB边向点B以3cm/s的速度移动,点Q从点C开始沿CD边向点D以2cm/s的速度移动,点P、Q从出发开始,经过几秒时,点P、Q、D组成的三角形是等腰三角形?
在长方形ABCD中,AB=16cm,BC=6cm,点P从A点开始沿AB边向点B以3cm/s的速度移动,点Q从点C开始沿CD边向点D以2cm/s的速度移动,点P、Q从出发开始,经过几秒时,点P、Q、D组成的三角形是等腰三角形?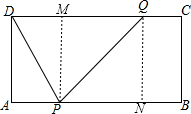 解:设时间为ts,过P作PM⊥CD于M,过Q作QN⊥AB于N,
解:设时间为ts,过P作PM⊥CD于M,过Q作QN⊥AB于N,32±4
| ||
| 14 |
16±2
| ||
| 7 |
16+2
| ||
| 7 |
| 16 |
| 3 |
16-2
| ||
| 7 |
-64±12
| ||
| 10 |
-32±6
| ||
| 5 |
-32-6
| ||
| 5 |
-32+6
| ||
| 5 |
16-2
| ||
| 7 |
-32+6
| ||
| 5 |


科目:初中数学 来源: 题型:
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| 姓名 | 一专项测试和6次选拔赛成绩 | ||||||
| 小明 | 603 | 589 | 602 | 596 | 604 | 612 | 608 |
| 小勇 | 597 | 580 | 597 | 630 | 590 | 631 | 596 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com