
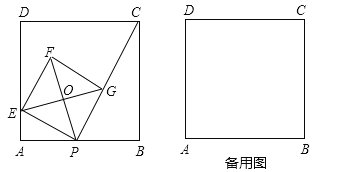
ЁОЬтФПЁПШчЭМЃЌвбжЊе§ЗНаЮABCDЕФБпГЄЮЊ4ЃЌЕуPЪЧABБпЩЯЕФвЛИіЖЏЕуЃЌСЌНгCPЃЌЙ§ЕуPзїPCЕФДЙЯпНЛADгкЕуEЃЌвд PEЮЊБпзїе§ЗНаЮPEFGЃЌЖЅЕуGдкЯпЖЮPCЩЯЃЌЖдНЧЯпEGЁЂPFЯрНЛгкЕуOЃЎ
ЃЈ1ЃЉШєAP=1ЃЌдђAE= ЃЛ
ЃЈ2ЃЉЂйЧѓжЄЃКЕуOвЛЖЈдкЁїAPEЕФЭтНгдВЩЯЃЛ
ЂкЕБЕуPДгЕуAдЫЖЏЕНЕуBЪБЃЌЕуOвВЫцжЎдЫЖЏЃЌЧѓЕуOОЙ§ЕФТЗОЖГЄЃЛ
ЃЈ3ЃЉдкЕуPДгЕуAЕНЕуBЕФдЫЖЏЙ§ГЬжаЃЌЁїAPEЕФЭтНгдВЕФдВаФвВЫцжЎдЫЖЏЃЌЧѓИУдВаФЕНABБпЕФОрРыЕФзюДѓжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉЂйжЄУїМћНтЮіЃЛЂк
ЃЛЃЈ2ЃЉЂйжЄУїМћНтЮіЃЛЂк![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() ЃЎ
ЃЎ
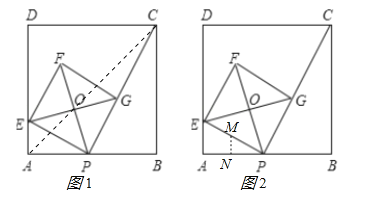
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉгЩе§ЗНаЮЕФаджЪЕУГіЁЯA=ЁЯB=ЁЯEPG=90ЁуЃЌPFЁЭEGЃЌAB=BC=4ЃЌЁЯOEP=45ЁуЃЌгЩНЧЕФЛЅгрЙиЯЕжЄГіЁЯAEP=ЁЯPBCЃЌЕУГіЁїAPEЁзЁїBCPЃЌЕУГіЖдгІБпГЩБШР§МДПЩЧѓГіAEЕФГЄЃЛ
ЃЈ2ЃЉЂйAЁЂPЁЂOЁЂEЫФЕуЙВдВЃЌМДПЩЕУГіНсТлЃЛ
ЂкСЌНгOAЁЂACЃЌгЩЙДЙЩЖЈРэЧѓГіAC=![]() ЃЌгЩдВжмНЧЖЈРэЕУГіЁЯOAP=ЁЯOEP=45ЁуЃЌжмГЄЕуOдкACЩЯЃЌЕБPдЫЖЏЕНЕуBЪБЃЌOЮЊACЕФжаЕуЃЌМДПЩЕУГіД№АИЃЛ
ЃЌгЩдВжмНЧЖЈРэЕУГіЁЯOAP=ЁЯOEP=45ЁуЃЌжмГЄЕуOдкACЩЯЃЌЕБPдЫЖЏЕНЕуBЪБЃЌOЮЊACЕФжаЕуЃЌМДПЩЕУГіД№АИЃЛ
ЃЈ3ЃЉЩшЁїAPEЕФЭтНгдВЕФдВаФЮЊMЃЌзїMNЁЭABгкNЃЌгЩШ§НЧаЮжаЮЛЯпЖЈРэЕУГіMN=![]() AEЃЌЩшAP=xЃЌдђBP=4ЉxЃЌгЩЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§ЧѓГіAEЕФБэДяЪНЃЌгЩЖўДЮКЏЪ§ЕФзюДѓжЕЧѓГіAEЕФзюДѓжЕЮЊ1ЃЌЕУГіMNЕФзюДѓжЕ=
AEЃЌЩшAP=xЃЌдђBP=4ЉxЃЌгЩЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§ЧѓГіAEЕФБэДяЪНЃЌгЩЖўДЮКЏЪ§ЕФзюДѓжЕЧѓГіAEЕФзюДѓжЕЮЊ1ЃЌЕУГіMNЕФзюДѓжЕ=![]() МДПЩЃЎ
МДПЩЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЁпЫФБпаЮABCDЁЂЫФБпаЮPEFGЪЧе§ЗНаЮЃЌ
ЁрЁЯA=ЁЯB=ЁЯEPG=90ЁуЃЌPFЁЭEGЃЌAB=BC=4ЃЌЁЯOEP=45ЁуЃЌ
ЁрЁЯAEP+ЁЯAPE=90ЁуЃЌЁЯBPC+ЁЯAPE=90ЁуЃЌ
ЁрЁЯAEP=ЁЯPBCЃЌЁрЁїAPEЁзЁїBCPЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌНтЕУЃКAE=
ЃЌНтЕУЃКAE=![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃК ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЂйЁпPFЁЭEGЃЌЁрЁЯEOF=90ЁуЃЌ
ЁрЁЯEOF+ЁЯA=180ЁуЃЌЁрAЁЂPЁЂOЁЂEЫФЕуЙВдВЃЌ
ЁрЕуOвЛЖЈдкЁїAPEЕФЭтНгдВЩЯЃЛ
ЂкСЌНгOAЁЂACЃЌШчЭМ1ЫљЪОЃК
ЁпЫФБпаЮABCDЪЧе§ЗНаЮЃЌЁрЁЯB=90ЁуЃЌЁЯBAC=45ЁуЃЌЁрAC=![]() =
=![]() ЃЌ
ЃЌ
ЁпAЁЂPЁЂOЁЂEЫФЕуЙВдВЃЌЁрЁЯOAP=ЁЯOEP=45ЁуЃЌ
ЁрЕуOдкACЩЯЃЌЕБPдЫЖЏЕНЕуBЪБЃЌOЮЊACЕФжаЕуЃЌOA=![]() AC=
AC=![]() ЃЌ
ЃЌ
МДЕуOОЙ§ЕФТЗОЖГЄЮЊ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЩшЁїAPEЕФЭтНгдВЕФдВаФЮЊMЃЌзїMNЁЭABгкNЃЌШчЭМ2ЫљЪОЃК
дђMNЁЮAEЃЌЁпME=MPЃЌЁрAN=PNЃЌЁрMN=![]() AEЃЌ
AEЃЌ
ЩшAP=xЃЌдђBP=4ЉxЃЌгЩЃЈ1ЃЉЕУЃКЁїAPEЁзЁїBCPЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌНтЕУЃКAE=
ЃЌНтЕУЃКAE= ![]() =
=![]() ЃЌ
ЃЌ
Ёрx=2ЪБЃЌAEЕФзюДѓжЕЮЊ1ЃЌДЫЪБMNЕФжЕзюДѓ=![]() ЁС1=
ЁС1=![]() ЃЌ
ЃЌ
МДЁїAPEЕФдВаФЕНABБпЕФОрРыЕФзюДѓжЕЮЊ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCКЭЁїDCBжаЃЌACгыBDЯрНЛгкЕуOЃЌЯТСаЫФзщЬѕМўжаЃЌВЛФмжЄУїЁїABCЁеЁїDCBЕФЪЧЃЈЁЁЁЁЃЉ

A.ABЃНDCЃЌACЃНDBB.ABЃНDCЃЌЁЯABCЃНЁЯDCB
C.BOЃНCOЃЌЁЯAЃНЁЯDD.ЁЯABDЃНЁЯDCAЃЌЁЯAЃНЁЯD
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAC=BC=6,ЁЯACBЃО90Ёу,ЁЯABCЕФЦНЗжЯпНЛACгкЕуDЃЌEЪЧABЩЯвЛЕуЃЌЧвBE=BCЃЌCFЁЮEDНЛBDгкЕуFЃЌСЌНгEF,ED.
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮCDEFЪЧСтаЮЃЎ
ЃЈ2ЃЉЕБЁЯACBЃН ЖШЪБЃЌЫФБпаЮCDEFЪЧе§ЗНаЮЃЌЧыИјгшжЄУїЃЛВЂЧѓДЫЪБе§ЗНаЮЕФБпГЄЁЃ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯA=90ЁуЃЌAB=ACЃЌBC=20ЃЌDEЪЧЁїABCЕФжаЮЛЯпЃЌЕуMЪЧБпBCЩЯвЛЕуЃЌBM=3ЃЌЕуNЪЧЯпЖЮMCЩЯЕФвЛИіЖЏЕуЃЌСЌНгDNЃЌMEЃЌDNгыMEЯрНЛгкЕуOЃЎШєЁїOMNЪЧжБНЧШ§НЧаЮЃЌдђDOЕФГЄЪЧ______ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
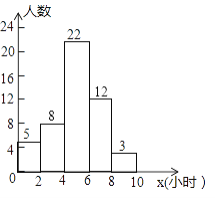
ЁОЬтФПЁПФГаЃЮЊСЫНтШЋаЃ1600УћбЇЩњУПжмПЮЭтЬхг§ЛюЖЏЪБМфЕФЧщПіЃЌЫцЛњЕїВщСЫЦфжаЕФВПЗжбЇЩњЃЌЖдетаЉбЇЩњУПжмПЮЭтЬхг§ЛюЖЏЪБМфxЃЈЕЅЮЛЃКаЁЪБЃЉНјааСЫЭГМЦЃЌИљОнЫљЕУЪ§ОнЛцжЦСЫвЛЗљЭГМЦЭМЃЌИљОнвдЩЯаХЯЂМАЭГМЦЭМНтД№ЯТСаЮЪЬт
ЃЈ1ЃЉБОДЮНгЪмЫцЛњГщбљЕїВщЕФбЇЩњШЫЪ§ЮЊ______ЃЛ
ЃЈ2ЃЉЧѓетаЉбЇЩњУПжмПЮЭтЬхг§ЛюЖЏЪБМфЕФЦНОљЪ§________ЃЛ
ЃЈ3ЃЉЙРМЦШЋаЃбЇЩњУПжмПЮЭтЬхг§ЛюЖЏЪБМфВЛЩйгк4аЁЪБЕФШЫЪ§________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫНтФГаЁЧјОгУёЕФШегУЕчЧщПіОгзЁдкаЁЧјЕФвЛУћЭЌбЇЫцЛњГщВщСЫ15ЛЇМвЭЅЕФШегУЕчСПЃЌОпЬхНсЙћШчЯТБэЫљЪОЃЎ
ШегУЕчСП/ЧЇЭпЪБ | 5 | 6 | 7 | 8 | 10 |
ЛЇЪ§ | 2 | 5 | 4 | 3 | 1 |
дђЙигкет15ЛЇМвЭЅЕФШегУЕчСПЃЌЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈ ЃЉ
A.жкЪ§ЪЧ10ЧЇЭпЪБB.ЦНОљЪ§ЪЧ7ЧЇЭпЪБ
C.жаЮЛЪ§ЪЧ6ЧЇЭпЪБD.жаЮЛЪ§ЪЧ7ЧЇЭпЪБ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDЕФБпГЄЪЧ3ЃЌBP=CQЃЌСЌНгAQЃЌDPНЛгкЕуOЃЌВЂЗжБ№гыБпCDЃЌBCНЛгкЕуFЃЌEЃЌСЌНгAEЃЌЯТСаНсТлЃКЂйAQЁЭDPЃЛЂкOA2=OEOPЃЛЂлSЁїAOD=SЫФБпаЮOECFЃЛЂмЕБBP=1ЪБЃЌtanЁЯOAE=![]() ЃЌЦфжае§ШЗНсТлЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ
ЃЌЦфжае§ШЗНсТлЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ

A. 1 B. 2 C. 3 D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвЪаКюеђЖўжааЃдАФкгавЛКЩЛЈГиЃЌКЩЛЈГиББВргавЛЫЎЫўЃЎОХФъМЖЪ§бЇаЫШЄаЁзщгћРћгУЫљбЇжЊЪЖВтСПЫЎЫўИпЖШЃЎВтСПЙ§ГЬШчЯТЃКЯШдкКЩЛЈГиФЯВрAЕугЩВтНЧвЧAEВтЕУЫўЖЅбіНЧЮЊ30ЁуЃЌдйдкКЩЛЈГиББВрBЕугЩВтНЧвЧBFВтЕУЫўЖЅбіНЧЮЊ45ЁуЃЌКЩЛЈГиABГЄЮЊ15УзЃЌВтНЧвЧИпОљЮЊ1.5УзЃЌвбжЊAЁЂBЁЂCШ§ЕудквЛЬѕжБЯпЩЯЃЌЧыИљОнвдЩЯЬѕМўЧѓЫўИпCDЃПЃЈБЃСєСНЮЛаЁЪ§ЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
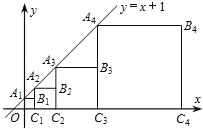
ЁОЬтФПЁПШчЭМЃЌжБЯп y=x+1 гы y жсНЛгкЕу A1ЃЌвд OA1ЮЊБп,дк y жсгвВрзїе§ЗНаЮ OA1B1C1ЃЌбгГЄ C1B1НЛжБЯп y=x+1 гкЕу A2ЃЌдйвд C1A2ЮЊБпзїе§ЗНаЮЃЌЁЃЌетаЉе§ЗНаЮгыжБЯп y=x+1 ЕФНЛЕуЗжБ№ЮЊ A1ЃЌA2ЃЌA3ЃЌЁЃЌAnЃЌдђЕу Bn ЕФзјБъЮЊ_______ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com