
【题目】课上教师呈现一个问题

甲、乙、丙三位同学用不同的方法添加辅助线解决问题,如下图:
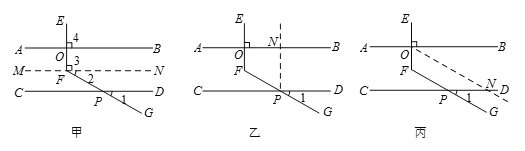
甲同学辅助线的做法和分析思路如下:

(1)请你根据乙同学所画的图形,描述辅助线的做法,并写出相应的分析思路.
辅助线:___________________;
分析思路:
(2)请你根据丙同学所画的图形,求∠EFG的度数.
【答案】(1)辅助线:过点P作PN∥EF交AB于点N.
分析思路:
①欲求∠EFG的度数,由辅助线作图可知,∠EFG=∠NPG,
因此,只需转化为求∠NPG的度数;
②欲求∠NPG的度数,由图可知只需转化为求∠1和∠2的度数;
③又已知∠1的度数,所以只需求出∠2的度数;
④由已知EF⊥AB,可得∠4=90°;
⑤由PN∥EF,可推出∠3=∠4;AB∥CD可推出∠2=∠3,由此可推∠2=∠4,
所以可得∠2的度数;
⑥从而可以求出∠EFG的度数.
(2)120°
【解析】(1)辅助线:过点P作PN∥EF交AB于点N.
分析思路:
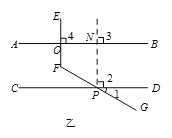
①欲求∠EFG的度数,由辅助线作图可知,∠EFG=∠NPG,
因此,只需转化为求∠NPG的度数;
②欲求∠NPG的度数,由图可知只需转化为求∠1和∠2的度数;
③又已知∠1的度数,所以只需求出∠2的度数;
④由已知EF⊥AB,可得∠4=90°;
⑤由PN∥EF,可推出∠3=∠4;AB∥CD可推出∠2=∠3,由此可推∠2=∠4,
所以可得∠2的度数;
⑥从而可以求出∠EFG的度数.
(2)过点O作ON∥FG
∵ON∥FG
∴∠EFG=∠EON ∠1=∠ONC=30°
∵AB∥CD
∴∠ONC=∠BON=30°
∵EF⊥AB
∴∠EOB=90°
∴∠EFG=∠EON=∠EOB+∠BON=90°+30°=120°


科目:初中数学 来源: 题型:
【题目】如图,在边长为6的等边△ABC中,AD是BC边上的中线,点E是△ABC内一个动点,且DE=2,将线段AE绕点A逆时针旋转60°得到AF,则DF的最小值是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北方某水果商店从南方购进一种水果,其进货成本是每吨0.4万元,根据市场调查这种水果在北方市场上的销售量y(吨)与每吨的销售价x(万元)之间的函数关系如下图所示:
(1)求出销售量y与每吨销售价x之间的函数关系式;
(2)如果销售利润为w(万元),请写出w与x之间的函数关系式;
(3)当每吨销售价为多少万元时,销售利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC 中,AB=15,AC=13,高 AD=12,则△ABC 的周长是( )
A. 42B. 32C. 42 或 32D. 42 或 37
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分别直方图和扇形统计图:

根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图
(2)求扇形统计图中m的值和E组对应的圆心角度数
(3)请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D在反比例函数y=![]() 的图象上,过点D作x轴的平行线交y轴于点B(0,3),过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=
的图象上,过点D作x轴的平行线交y轴于点B(0,3),过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=![]() .
.
(1)求反比例函数y=![]() 和直线y=kx+b的解析式;
和直线y=kx+b的解析式;
(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;
(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA于点M,求∠BMC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型企业为了保护环境,准备购买A、B两种型号的污水处理设备共8台,用于同时治理不同成分的污水,若购买A型2台、B型3台需54万,购买A型4台、B型2台需68万元.
(1)求出A型、B型污水处理设备的单价;
(2)经核实,一台A型设备一个月可处理污水220吨,一台B型设备一个月可处理污水190吨,如果该企业每月的污水处理量不低于1565吨,请你为该企业设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为( )

A.2B.2.2C.2.4D.2.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com