
 如图,已知直线y=$\frac{1}{3}$x+1与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.
如图,已知直线y=$\frac{1}{3}$x+1与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.分析 (1)由直线解析式可求得A、B坐标,由旋转的性质可求得OC和OD,则可求得AD的长;
(2)由勾股定理可求得CD的长,由条件可证得MD=MO,则可得M为CD的中点,利用待定系数法可求得直线OM的解析式;
(3)根据直线OM的解析式可设出直线AM的解析式,把A点坐标代入可求得直线AM的解析式.
解答 解:
(1)在y=$\frac{1}{3}$x+1中,令y=0可得$\frac{1}{3}$x+1=0,解得x=-3,
令x=0可得y=1,
∴A(-3,0),B(0,1),
∵将△AOB绕点O顺时针旋转90°后得到△COD,
∴OC=OA=3,OD=OB=1,
∴C(0,3),AD=OA+OD=3+1=4;
(2)∵CM=OM,
∴∠OCM=∠MOC,
∵∠OCM+∠MDO=90°=∠COM+∠MOD,
∴∠MOD=∠MDO,
∴MD=OM,
∴M为CD中点,
∴M($\frac{1}{2}$,$\frac{3}{2}$),
设直线OM解析式为y=kx,
∴$\frac{3}{2}$=$\frac{1}{2}$k,解得k=3,
∴直线OM解析式为y=3x;
(3)可设平移后的OM的解析式为y=3x+b,
∵OM向左平移后经过点A,
∴0=-9+b,解得b=9,
∴平移后的OM的解析式为y=3x+9.
点评 本题为一次函数的综合应用,涉及旋转的性质、勾股定理、等腰三角形的性质和判定、待定系数法及平移的性质.在(1)中利用旋转的性质求得OC、OD的长是解题的关键,在(2)中求得M点的坐标是解题的关键,在(3)中利用平移前后直线解析式中的k相等是解题的关键.本题考查知识点较多,综合性较强,难度适中.


科目:初中数学 来源: 题型:解答题
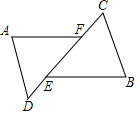 如图所示,△ADF和△BCE中,∠A=∠B,点D,E,F,C在同一直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF.请用其中两个关系式作为条件,另一个作为结论,写出的一个正确结论,并说明它正确的理由.
如图所示,△ADF和△BCE中,∠A=∠B,点D,E,F,C在同一直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF.请用其中两个关系式作为条件,另一个作为结论,写出的一个正确结论,并说明它正确的理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
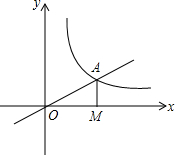 如图,正比例y=$\frac{1}{2}$x的图象与y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知△OAM的面积为1.如果B为及比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,P为x轴上一点,求使PA+PB的值最小时点P坐标.
如图,正比例y=$\frac{1}{2}$x的图象与y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知△OAM的面积为1.如果B为及比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,P为x轴上一点,求使PA+PB的值最小时点P坐标.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
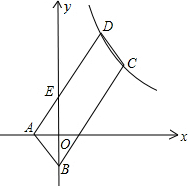 如图,?ABCD的顶点A、B的坐标分别是A(-1,0),B(0,-3),顶点C、D在双曲线y=$\frac{k}{x}$上,边AD交y轴于点E,且?ABCD的面积是△ABE面积的8倍,则k=36.
如图,?ABCD的顶点A、B的坐标分别是A(-1,0),B(0,-3),顶点C、D在双曲线y=$\frac{k}{x}$上,边AD交y轴于点E,且?ABCD的面积是△ABE面积的8倍,则k=36.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3),△AOB绕点O逆时针旋转90°后得到△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3),△AOB绕点O逆时针旋转90°后得到△A1OB1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com