Question

如图，AB为的直径，点C在⊙O上，点P是直径AB上的一点（不与A，B重合），过点P作AB的垂线交BC的延长线于点Q。

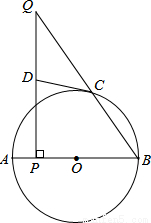
（1）在线段PQ上取一点D，使DQ=DC，连接DC，试判断CD与⊙O的位置关系，并说明理由。

（2）若cosB=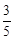，BP=6，AP=1，求QC的长。

 

Answer 1

【答案】

解：（1）CD是⊙O的切线,。理由如下：

连接OC，

∵OC=OB，∴∠B=∠BCO。

又∵DC=DQ，∴∠Q=∠DCQ。

∵PQ⊥AB，∴∠QPB=90°。

∴∠B+∠Q=90°。∴∠BCO +∠DCQ =90°。

∴∠DCO=∠QCB－(∠BCO +∠DCQ)=180°－90°=90°。

∴OC⊥DC。

∵OC是⊙O的半径，∴CD是⊙O的切线。

（2）连接AC，

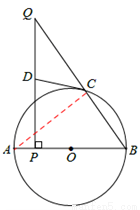
∵AB是⊙O的直径，∴∠ACB=90°。

在Rt△ABC中，BC=ABcosB=(AP+BP) cosB=(1+6)×，

在Rt△BPQ中，，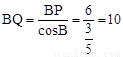

∴。

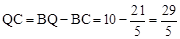【解析】

试题分析：（1）应用等腰三角形等边对等角的性质、直角三角形两锐角到余的关系和平角的性质，证明∠DCO=90°，即可得出结论。

（2）在Rt△ABC和Rt△BPQ中应用锐角三角函数求出BC和BQ的长，由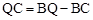求出结果。