
分析 (1)先把各二次根式化简为最简二次根式,然后合并即可;
(2)先利用平方差公式计算,再利用二次根式的性质化简后合并即可.
解答 解:(1)原式=4$\sqrt{3}$-$\sqrt{2}$-$\frac{2\sqrt{3}}{3}$+$\sqrt{2}$
=$\frac{10\sqrt{3}}{3}$;
(2)原式=2+1-$\sqrt{3}$+$\sqrt{3}$($\sqrt{3}$-1)•$\frac{\sqrt{3}+1}{\sqrt{3}}$
=3-$\sqrt{3}$+3-1
=5-$\sqrt{3}$.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:填空题
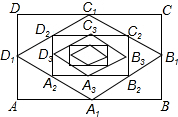 如图,在矩形ABCD中,AB=16,BC=12,顺次连结各边中点,得菱形A1B1C1D1;再顺次连结菱形A1B1C1D1的各边中点,得矩形A2B2C2D2;再顺次连结矩形A2B2C2D2的各边中点,得菱形A3B3C3D3;…这样继续下去.则图中的四边形A8B8C8D8的周长等于4,图中的四边形AnBnCnDn的面积等于192×($\frac{1}{2}$)n.
如图,在矩形ABCD中,AB=16,BC=12,顺次连结各边中点,得菱形A1B1C1D1;再顺次连结菱形A1B1C1D1的各边中点,得矩形A2B2C2D2;再顺次连结矩形A2B2C2D2的各边中点,得菱形A3B3C3D3;…这样继续下去.则图中的四边形A8B8C8D8的周长等于4,图中的四边形AnBnCnDn的面积等于192×($\frac{1}{2}$)n.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知一次函数y=2x-4.
已知一次函数y=2x-4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 小明的研究报告 | 小红的研究报告 | |
| 测量图例 | 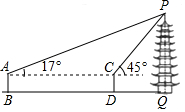 | 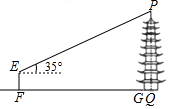 |
| 测量过程 | 如图,测角仪AB、CD的高度均为1.6m,分别测得古塔顶端的仰角为17°、45°,测角仪底端的距离(BD)为69m. | 如图,测角仪EF的高度为1.6m,测得古塔顶端的仰角为35°,测角仪所在位置与古塔底部边缘的最短距离(FG)为38.3m. |
| 参考数据 | sin17°≈0.29,cos17°≈0.96, tan17°≈0.31,$\sqrt{2}$≈1.41 | sin35°≈0.57,cos35°≈0.82, tan35°≈0.70 |
| 数据处理 | 32.6 | PQ=38.3×tan35°+1.6≈28.41(m) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
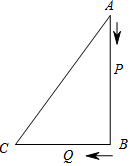 如图,已知△ABC中,∠B=90°,AB=12cm,BC=9cm,P,Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
如图,已知△ABC中,∠B=90°,AB=12cm,BC=9cm,P,Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com