
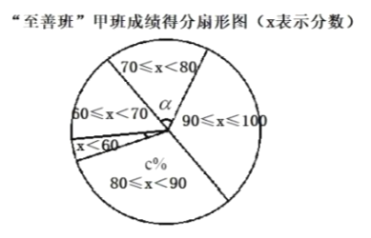
”¾ĢāÄæ”æ”°¾»Ńļ”±Ė®¾»»ÆÓŠĻŽ¹«Ė¾ÓĆ160ĶņŌŖ£¬×÷ĪŖŠĀ²śĘ·µÄŃŠ·¢·ŃÓĆ£¬³É¹¦ŃŠÖĘ³öĮĖŅ»ÖÖŹŠ³”¼±ŠčµÄŠ”ŠĶĖ®¾»»Æ²śĘ·£¬ŅŃÓŚµ±ÄźĶ¶ČėÉś²ś²¢½ųŠŠĻśŹŪ£®ŅŃÖŖÉś²śÕāÖÖŠ”ŠĶĖ®¾»»Æ²śĘ·µÄ³É±¾ĪŖ4ŌŖ/¼ž£¬ŌŚĻśŹŪ¹ż³ĢÖŠ·¢ĻÖ£ŗĆæÄźµÄÄźĻśŹŪĮæ![]() (Ķņ¼ž)ÓėĻśŹŪ¼Ūøńx£ØŌŖ/¼ž£©µÄ¹ŲĻµČēĶ¼ĖłŹ¾£¬ĘäÖŠABĪŖ·“±ČĄżŗÆŹżĶ¼ĻóµÄŅ»²æ·Ö£¬BCĪŖŅ»“ĪŗÆŹżĶ¼ĻóµÄŅ»²æ·Ö£®Éč¹«Ė¾ĻśŹŪÕāÖÖĖ®¾»»Æ²śĘ·µÄÄźĄūČóĪŖz£ØĶņŌŖ£©£®£Ø×¢£ŗČōÉĻŅ»ÄźÓÆĄū£¬ŌņÓÆĄū²»¼ĘČėĻĀŅ»ÄźµÄÄźĄūČó£»ČōÉĻŅ»Äźæ÷Ėš£¬Ōņæ÷Ėš¼Ę×÷ĻĀŅ»ÄźµÄ³É±¾£®£©
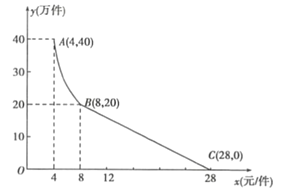
(Ķņ¼ž)ÓėĻśŹŪ¼Ūøńx£ØŌŖ/¼ž£©µÄ¹ŲĻµČēĶ¼ĖłŹ¾£¬ĘäÖŠABĪŖ·“±ČĄżŗÆŹżĶ¼ĻóµÄŅ»²æ·Ö£¬BCĪŖŅ»“ĪŗÆŹżĶ¼ĻóµÄŅ»²æ·Ö£®Éč¹«Ė¾ĻśŹŪÕāÖÖĖ®¾»»Æ²śĘ·µÄÄźĄūČóĪŖz£ØĶņŌŖ£©£®£Ø×¢£ŗČōÉĻŅ»ÄźÓÆĄū£¬ŌņÓÆĄū²»¼ĘČėĻĀŅ»ÄźµÄÄźĄūČó£»ČōÉĻŅ»Äźæ÷Ėš£¬Ōņæ÷Ėš¼Ę×÷ĻĀŅ»ÄźµÄ³É±¾£®£©
£Ø1£©ĒėĒó³öy£ØĶņ¼ž£©Óėx£ØŌŖ/¼ž£©Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£»
£Ø2£©Ēó³öµŚŅ»ÄźÕāÖÖĖ®¾»»Æ²śĘ·µÄÄźĄūČóz£ØĶņŌŖ£©Óėx£ØŌŖ/¼ž£©Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Ēó³öµŚŅ»ÄźÄźĄūČóµÄ×ī“óÖµ£»
£Ø3£©¼ŁÉč¹«Ė¾µÄÕāÖÖĖ®¾»»Æ²śĘ·µŚŅ»ÄźĒ”ŗĆ°“ÄźĄūČóz£ØĶņŌŖ£©Č”µĆ×ī“óÖµŹ±½ųŠŠĻśŹŪ£¬ĻÖøł¾ŻµŚŅ»ÄźµÄÓÆæ÷Ēéæö£¬¾ö¶ØµŚ¶žÄź½«ÕāÖÖĖ®¾»»Æ²śĘ·Ć漞µÄĻśŹŪ¼Ūøńx£ØŌŖ£©¶ØŌŚ8ŌŖŅŌÉĻ£Ø![]() £©£¬µ±µŚ¶žÄźµÄÄźĄūČó²»µĶÓŚ103ĶņŌŖŹ±£¬Ēė½įŗĻÄźĄūČóz£ØĶņŌŖ£©ÓėĻśŹŪ¼Ūøńx£ØŌŖ/¼ž£©µÄŗÆŹżŹ¾ŅāĶ¼£¬ĒóĻśŹŪ¼Ūøńx£ØŌŖ/¼ž£©µÄȔֵ·¶Ī§£®
£©£¬µ±µŚ¶žÄźµÄÄźĄūČó²»µĶÓŚ103ĶņŌŖŹ±£¬Ēė½įŗĻÄźĄūČóz£ØĶņŌŖ£©ÓėĻśŹŪ¼Ūøńx£ØŌŖ/¼ž£©µÄŗÆŹżŹ¾ŅāĶ¼£¬ĒóĻśŹŪ¼Ūøńx£ØŌŖ/¼ž£©µÄȔֵ·¶Ī§£®
”¾“š°ø”æ£Ø1£©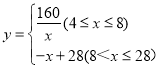 £»£Ø2£©µ±4”Üx”Ü8Ź±£¬
£»£Ø2£©µ±4”Üx”Ü8Ź±£¬![]() £»µ±8£¼x”Ü28Ź±£¬
£»µ±8£¼x”Ü28Ź±£¬![]() £»µ±Ć漞µÄĻśŹŪ¼Ūøń¶Ø ĪŖ16ŌŖŹ±£¬µŚŅ»ÄźµÄÄźĄūČó×ī“óĪŖ-16ĶņŌŖ£»£Ø3£©µ±11”Üx”Ü21Ź±£¬µŚ¶žÄźµÄÄźĄūČóz²»µĶÓŚ103ĶņŌŖ£®
£»µ±Ć漞µÄĻśŹŪ¼Ūøń¶Ø ĪŖ16ŌŖŹ±£¬µŚŅ»ÄźµÄÄźĄūČó×ī“óĪŖ-16ĶņŌŖ£»£Ø3£©µ±11”Üx”Ü21Ź±£¬µŚ¶žÄźµÄÄźĄūČóz²»µĶÓŚ103ĶņŌŖ£®
”¾½āĪö”æ
£Ø1£©½«µćAµÄ×ų±ź“śČė·“±ČĄżŗÆŹżĒó½ā¼“æÉĒó³ö·“±ČĄżŗÆŹżµÄ½āĪöŹ½£¬ŌŁ½«µćBŗĶµćCµÄ×ų±ź“śČėŅ»“ĪŗÆŹżĒó½ā¼“æÉµĆ³öŅ»“ĪŗÆŹżµÄ½āĪöŹ½£»
£Ø2£©øł¾Ż¹«Ź½”°×ÜĄūČó=µ„¼žĄūČó”ĮŹżĮæ”±¼“æÉµĆ³ö½āĪöŹ½£¬ŌŁøł¾Ż¶ž“ĪŗÆŹżµÄŠŌÖŹ¼“æÉµĆ³ö“š°ø£»
£Ø3£©ĻČĒó³öµŚ¶žÄźµÄÄźĄūČó¹«Ź½ŌŁĮīÄźĄūČóµČÓŚ103£¬½āŅ»ŌŖ¶ž“Ī·½³Ģ²¢½įŗĻĶ¼ĻńŠŌÖŹ¼“æÉµĆ³ö“š°ø£®
½ā£ŗ£Ø1£©µ±4”Üx”Ü8£¬Éčy=![]() £¬½«A£Ø4£¬40£©“śČė
£¬½«A£Ø4£¬40£©“śČė
µĆk=4”Į40=160£¬
ĖłŅŌyÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½ĪŖ£ŗy=![]() £¬
£¬
µ±8£¼x”Ü28Ź±£¬Éčy=kx+b£¬
½«B£Ø8£¬20£©”¢C£Ø28£¬0£©“śČėµĆ
![]() £¬
£¬
½āµĆ![]() £¬
£¬
”ąyÓėxÖ®¼äµÄŗÆŹż¹ŲĻµĪŖy=-x+28£¬
”ą×ŪÉĻĖłŹöµĆ£ŗ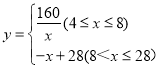 £»
£»
£Ø2£©µ±4”Üx”Ü8Ź±£¬![]() £¬
£¬
”ßzĖę×ÅxµÄŌö“ó¶ųŌö“ó£¬
”ąµ±x=8Ź±£¬z×ī“óÖµĪŖ-80£¬
µ±8£¼x”Ü28Ź±£¬![]()
”ąµ±x=16Ź±£¬z×ī“óÖµĪŖ-16£¬
”ß-80£¼-16£¬
”ąµ±Ć漞µÄĻśŹŪ¼Ūøń¶Ø ĪŖ16ŌŖŹ±£¬µŚŅ»ÄźµÄÄźĄūČó×ī“óĪŖ-16ĶņŌŖ£»
£Ø3£©”ßµŚŅ»ÄźµÄÄźĄūČóĪŖ-16ĶņŌŖ£¬
”ą-16ĶņŌŖÓ¦×÷ĪŖµŚ¶žÄźµÄ³É±¾£¬
”ąµŚ¶žÄźµÄÄźĄūČóz=£Øx-4£©£Ø-x+28£©-16=![]() £¬
£¬
Įīz=103£¬Ōņ![]() =103£¬
=103£¬
½āµĆ![]() £¬
£¬
ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬»³özÓėxµÄŗÆŹżŹ¾ŅāĶ¼ČēĶ¼£¬
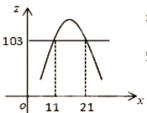
¹Ū²ģæÉÖŖ£ŗz”Ż103Ź±£¬11”Üx”Ü21£¬
”ąµ±11”Üx”Ü21Ź±£¬µŚ¶žÄźµÄÄźĄūČóz²»µĶÓŚ103ĶņŌŖ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
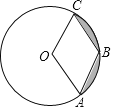
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ”ŃOµÄ°ė¾¶ŹĒ2£¬µćA”¢B”¢CŌŚ”ŃOÉĻ£¬ČōĖıߊĪOABCĪŖĮāŠĪ£¬ŌņĶ¼ÖŠŅõÓ°²æ·ÖĆ껿ĪŖ£Ø””””£©
A. ![]() ¦Š©2
¦Š©2![]() B.
B. ![]() ¦Š©
¦Š©![]() C.
C. ![]() ¦Š©2
¦Š©2![]() D.
D. ![]() ¦Š©
¦Š©![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÄ³ÖŠŃ§³õȿ𼶻ż¼«ĶĘ½ų×ß°ąÖĘ½Ģѧ£®ĪŖĮĖĮĖ½āŅ»¶ĪŹ±¼äŅŌĄ“£¬”°ÖĮÉĘ°ą”±µÄѧĻ°Š§ ¹ū£¬Äź¼¶×éÖÆĮĖ¶ą“Ī¶ØŹ±²āŹŌ£¬ĻÖĖ껜єȔ¼×”¢ŅŅĮ½øö”°ÖĮÉĘ°ą”±£¬“ÓÖŠø÷³éČ”![]() ĆūĶ¬Ń§ŌŚÄ³Ņ»“Ī¶ØŹ±²āŹŌÖŠµÄŹżŃ§³É¼Ø£¬Ęä½į¹ū¼ĒĀ¼ČēĻĀ£ŗ
ĆūĶ¬Ń§ŌŚÄ³Ņ»“Ī¶ØŹ±²āŹŌÖŠµÄŹżŃ§³É¼Ø£¬Ęä½į¹ū¼ĒĀ¼ČēĻĀ£ŗ
ŹÕ¼ÆŹż¾Ż£ŗ
”°ÖĮÉĘ°ą”±¼×°ą![]() µÄĆūĶ¬Ń§µÄŹżŃ§³É¼ØĶ³¼Ę£ØĀś·ÖĪŖ 100 ·Ö£©£Øµ„Ī»£ŗ·Ö£©
µÄĆūĶ¬Ń§µÄŹżŃ§³É¼ØĶ³¼Ę£ØĀś·ÖĪŖ 100 ·Ö£©£Øµ„Ī»£ŗ·Ö£©
![]()
![]()
”°ÖĮÉĘ°ą”±ŅŅ°ąµÄ![]() ĆūĶ¬Ń§µÄŹżŃ§³É¼ØĶ³¼Ę£ØĀś·ÖĪŖ 100 ·Ö£©£Øµ„Ī»£ŗ·Ö£©
ĆūĶ¬Ń§µÄŹżŃ§³É¼ØĶ³¼Ę£ØĀś·ÖĪŖ 100 ·Ö£©£Øµ„Ī»£ŗ·Ö£©
![]()
![]()
ÕūĄķŹż¾Ż£ŗ£Ø³É¼ØµĆ·ÖÓĆ![]() ±ķŹ¾£©
±ķŹ¾£©
·ÖŹż ŹżĮæ °ą¼¶ |
|
|
|
|
|
¼×°ą£ØČĖŹż£© | 1 | 3 | 4 | 6 | 6 |
ŅŅ°ą£ØČĖŹż£© | 1 | 1 | 8 | 6 | 4 |
·ÖĪöŹż¾Ż£¬²¢»Ų“šĻĀĮŠĪŹĢā£ŗ
![]() Ķź³ÉĻĀ±ķ£ŗ
Ķź³ÉĻĀ±ķ£ŗ
Ę½¾łŹż | ÖŠĪ»Źż | ÖŚŹż | |
¼×°ą |
|
|
|
ŅŅ°ą |
|
|
|
![]() ŌŚ”°ÖĮÉĘ°ą”±¼×°ąµÄÉČŠĪĶ¼ÖŠ£¬ ³É¼ØŌŚ
ŌŚ”°ÖĮÉĘ°ą”±¼×°ąµÄÉČŠĪĶ¼ÖŠ£¬ ³É¼ØŌŚ![]() µÄÉČŠĪÖŠ£¬Ėł¶ŌµÄŌ²ŠÄ½Ē
µÄÉČŠĪÖŠ£¬Ėł¶ŌµÄŌ²ŠÄ½Ē![]() µÄ¶ČŹżĪŖ £® ¹Ą¼ĘČ«²æ”°ÖĮÉĘ°ą”±µÄ
µÄ¶ČŹżĪŖ £® ¹Ą¼ĘČ«²æ”°ÖĮÉĘ°ą”±µÄ![]() ČĖÖŠÓÅŠćČĖŹżĪŖ ČĖ£®£Ø
ČĖÖŠÓÅŠćČĖŹżĪŖ ČĖ£®£Ø![]() ·Ö¼°ŅŌÉĻĪŖÓÅŠć£©£®
·Ö¼°ŅŌÉĻĪŖÓÅŠć£©£®
![]() øł¾ŻŅŌÉĻŹż¾Ż£¬ÄćČĻĪŖ”°ÖĮÉĘ°ą”± °ą£ØĢī”°¼×”±»ņ”°ŅŅ”±£©ĖłŃ”Č”×öŃł±¾ µÄĶ¬Ń§µÄѧĻ°Š§¹ūøüŗĆŅ»Š©£¬ÄćĖł×öÅŠ¶ĻµÄĄķÓÉŹĒ£ŗ
øł¾ŻŅŌÉĻŹż¾Ż£¬ÄćČĻĪŖ”°ÖĮÉĘ°ą”± °ą£ØĢī”°¼×”±»ņ”°ŅŅ”±£©ĖłŃ”Č”×öŃł±¾ µÄĶ¬Ń§µÄѧĻ°Š§¹ūøüŗĆŅ»Š©£¬ÄćĖł×öÅŠ¶ĻµÄĄķÓÉŹĒ£ŗ
¢Ł
¢Ś
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŗÆŹż![]() £¬Š”ĄīĶ¬Ń§¶ŌøĆŗÆŹżµÄĶ¼ĻóÓėŠŌÖŹ½ųŠŠĮĖĢ½¾æ£¬ĻĀĆęŹĒŠ”ĄīĶ¬Ń§Ģ½¾æµÄ¹ż³Ģ£¬²¹³äĶźÕū£ŗ
£¬Š”ĄīĶ¬Ń§¶ŌøĆŗÆŹżµÄĶ¼ĻóÓėŠŌÖŹ½ųŠŠĮĖĢ½¾æ£¬ĻĀĆęŹĒŠ”ĄīĶ¬Ń§Ģ½¾æµÄ¹ż³Ģ£¬²¹³äĶźÕū£ŗ
£Ø1£©Ö±½ÓŠ“³ö×Ō±äĮæxµÄȔֵ·¶Ī§£ŗ__________£»
£Ø2£©ĻĀ±ķŹĒyÓėxµÄ¼ø×é¶ŌÓ¦Öµ£ŗ
x | ” | -4 | -1 | 0 |
| 1 |
|
| 3 |
| 4 | 5 | n | ” |
y | ” |
| m |
| 0 | -1 | -4 | 8 | 5 | 4 |
| 3 |
| ” |
Ōņm=””””£¬n=””””£»
£Ø3£©ČēĶ¼ĖłŹ¾£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxoyÖŠ£¬Ćč³öŅŌÉĻ±ķÖŠø÷¶Ō¶ŌÓ¦ÖµĪŖ×ų±źµÄµć£¬²¢øł¾ŻĆč³öµÄµć£¬»³öøĆŗÆŹżµÄĶ¼Ļó£»
£Ø4£©¹Ū²ģŗÆŹżĶ¼ĻóæÉÖŖ£ŗøĆŗÆŹżĶ¼ĻóµÄ¶Ō³ĘÖŠŠÄµÄ×ų±źŹĒ______£»
£Ø5£©µ±![]() Ź±£¬¹ŲÓŚxµÄ·½³Ģ
Ź±£¬¹ŲÓŚxµÄ·½³Ģ![]() ÓŠŹµŹż½ā£¬Ö±½ÓŠ“³ökµÄȔֵ·¶Ī§_______£®
ÓŠŹµŹż½ā£¬Ö±½ÓŠ“³ökµÄȔֵ·¶Ī§_______£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ”°ŃĢ»ØČżŌĀĻĀŃļÖŻ”±-----ŃļÖŻČĖ½ÜµŲĮ飬ŹĒÖųĆūµÄĀĆÓĪ³ĒŹŠ£¬¼Ģ»ń”°ĮŖŗĻ¹śČĖ¾Ó½±”±ŗó£¬2019ÄźÓÖ»ń”°ŹĄ½ēĆĄŹ³Ö®¶¼”±µÄŹāČŁ£®”°ĪåŅ»”±³¤¼ŁĘŚ¼ä£¬Ä³²ĶŅūĘóŅµĪŖ»¶ÓĶāµŲÓĪæĶ£¬ĶĘ³öĮĖŅ»øö¾Ķ²Ķ³ź±ö»ī¶Æ£ŗŅ»Ö»²»ĶøĆ÷µÄ“ü×Ó֊װӊ·Ö±š±ź×ÅA”¢B”¢C”¢D×ÖÄøµÄĖÄøöĒņ£¬·Ö±š¶ŌÓ¦ŃļÖŻµÄĖÄÖÖĆĄŹ³£ŗA--ŃļÖŻ½“²Ė”¢ B--ŃļÖŻ°ü×Ó”¢C--ŃļÖŻĄĻ¶ģ”¢D--ŃļÖŻ³“·¹£¬ÕāŠ©Ēņ³ż×ÖÄø±ź¼ĒĶāĘäÓą¶¼ĻąĶ¬£®ÓĪæĶĻū·ŃæɲĪÓė»ī¶Æ£ŗµ„±ŹĻū·ŃĀś600ŌŖæÉŅ»“ĪĆž³öŅ»øöĒņ»ńČ”Ņ»ÖÖĻąÓ¦µÄĆĄŹ³£¬µ„±ŹĻū·ŃĀś1000ŌŖæÉŅ»“ĪĆž³öĮ½øöĒņ»ńČ”Į½ÖÖĻąÓ¦µÄĆĄŹ³£¬µ„±ŹĻū·ŃĀś1300ŌŖæÉŅ»“ĪĆž³öČżøöĒņ»ńȔȿÖÖĻąÓ¦µÄĆĄŹ³£¬µ„±ŹĻū·ŃĀś1500ŌŖæÉŅ»“Ī»ńČ”ĖÄĻī½±Ę·£®Ä³ÓĪæĶĻū·ŃĮĖ1200ŌŖ£¬²Ī¼ÓÕāøö»ī¶Æ£¬ĒėÓĆŹ÷דĶ¼»ņĮŠ±ķµÄ·½Ź½ĮŠ³öĖū»ńµĆĆĄŹ³µÄĖłÓŠæÉÄܽį¹ū£¬²¢Ēó³ö»ńµĆŃļÖŻ°ü×ÓŗĶŃļÖŻĄĻ¶ģµÄøÅĀŹ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¶Ō¶ž“ĪŗÆŹży£½x2+2mx+1£¬µ±0£¼x”Ü4Ź±ŗÆŹżÖµ×ÜŹĒ·ĒøŗŹż£¬ŌņŹµŹżmµÄȔֵ·¶Ī§ĪŖ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬”ŃOµÄ°ė¾¶ĪŖr£Ør£¾0£©£®øų³öČēĻĀ¶ØŅå£ŗČōĘ½ĆęÉĻŅ»µćPµ½Ō²ŠÄOµÄ¾ąĄėd£¬Āś×ć![]() £¬Ōņ³ĘµćPĪŖ”ŃOµÄ”°ĖęŠÄµć”±£®
£¬Ōņ³ĘµćPĪŖ”ŃOµÄ”°ĖęŠÄµć”±£®

£Ø1£©µ±”ŃOµÄ°ė¾¶r£½2Ź±£¬A£Ø3£¬0£©£¬B£Ø0£¬4£©£¬C£Ø©![]() £¬2£©£¬D£Ø
£¬2£©£¬D£Ø![]() £¬©
£¬©![]() £©ÖŠ£¬”ŃOµÄ”°ĖęŠÄµć”±ŹĒ_____£»
£©ÖŠ£¬”ŃOµÄ”°ĖęŠÄµć”±ŹĒ_____£»
£Ø2£©ČōµćE£Ø4£¬3£©ŹĒ”ŃOµÄ”°ĖęŠÄµć”±£¬Ēó”ŃOµÄ°ė¾¶rµÄȔֵ·¶Ī§£»
£Ø3£©µ±”ŃOµÄ°ė¾¶r£½2Ź±£¬Ö±Ļßy£½x+b£Øb”Ł0£©ÓėxÖį½»ÓŚµćM£¬ÓėyÖį½»ÓŚµćN£¬ČōĻ߶ĪMNÉĻ“ęŌŚ”ŃOµÄ”°ĖęŠÄµć”±£¬Ö±½ÓŠ“³öbµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
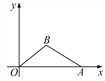
”¾ĢāÄæ”æČēĶ¼£¬ŌŚÖ±½Ē×ų±źĻµÄŚ£¬OĪŖŌµć£¬µćAµÄ×ų±źĪŖ(10£¬0)£¬µćBŌŚµŚŅ»ĻóĻŽÄŚ£¬BO£½5£¬sin”ĻBOA£½![]() . Ēó£ŗ(1)µćBµÄ×ų±ź£»(2)cos”ĻBAOµÄÖµ£®
. Ēó£ŗ(1)µćBµÄ×ų±ź£»(2)cos”ĻBAOµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ”°2018ŗ¼ÖŻĀķĄĖɾŗČü”±µÄøöČĖ¾ŗČüĻīÄæ¹²ÓŠČżĻī£ŗA£®”°ĀķĄĖÉ”±£¬B£®”°°ė³ĢĀķĄĖÉ”±£¬C£®”°ĆŌÄćĀķĄĖÉ”±£®Š”Ć÷ŗĶŠ”øÕ²Ī¼ÓĮĖøĆČüŹĀµÄÖ¾ŌøÕß·žĪń¹¤×÷£¬×éĪÆ»įĖ껜½«Ö¾ŌøÕß·ÖÅäµ½ČżøöĻīÄæ×飮
£Ø1£©Š”Ć÷±»·ÖÅäµ½”°ĆŌÄćĀķĄĖÉ”±ĻīÄæ×éµÄøÅĀŹĪŖ![]() ______£®
______£®
£Ø2£©ĒėÓĆ»Ź÷דĶ¼»ņĮŠ±ķµÄ·½·Ø£¬Ēó³öŠ”Ć÷ŗĶŠ”øÕ±»·ÖÅäµ½Ķ¬Ņ»ĻīÄæ×éµÄøÅĀŹ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com