
【题目】(8分)如图,在Rt△ABC中,∠ACB=Rt∠。
(1)请用直尺和圆规,过点C作AB边上的高线,交AB于D,作∠B的角平分线,交AC于E,交CD与F。
(2)△CEF是什么三角形,请说明理由
【答案】 (1) 图略;(2)等腰三角形,理由略
【解析】试题分析:(1)直接利用垂线的作法以及角平分线的作法得出D,E,F,点的位置;(2)根再由据对顶角的性质和和直角三角形两锐角互余的性质可得∠CFE=∠DFB=90°﹣∠FBD,
∠CEB=∠A+∠FBA=90°﹣∠CBE=90°﹣∠EBA=∠BFD,即可得∠CEF=∠CFE,由此即可得结论.
试题解析:
(1)如图所示:点D,E,F即为所求;
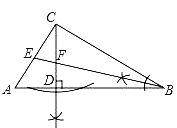
(2)△CEF是等腰三角形,
理由:∵∠CFE=∠DFB=90°﹣∠FBD,
∠CEB=∠A+∠FBA=90°﹣∠CBE=90°﹣∠EBA=∠BFD,
∴∠CEF=∠CFE,
∴△CEF是等腰三角形.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】(1)在如图所示的直角坐标系中,有一个三角形△ABC。把△ABC向下平移6个单位,得到△A1B1C1,再作△A1B1C1关于y轴的对称图形△A2B2C2,请在直角坐标系中画出△A1B1C1与△A2B2C2;
(2)写出A2、B2、C2的坐标;
(3)求出△A2B2C2的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
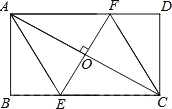
【题目】(2016广西省贺州市第23题)如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=![]() ,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016山东省泰安市第22题)如图,半径为3的⊙O与Rt△AOB的斜边AB切于点D,交OB于点C,连接CD交直线OA于点E,若∠B=30°,则线段AE的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了进行资源的再利用,学校准备针对库存的桌椅进行维修,现有甲、乙两木工组,甲每天修桌凳14 套,乙每天比甲多7套,甲单独修完这些桌凳比乙单独修完多用20天.学校每天付甲组80元修理费,付乙组120元修理费.
(1)请问学校库存多少套桌凳?
(2)在修理过程中,学校要派一名工人进行质量监督,学校负担他每天10元生活补助费,现有三种修理方案:①由甲单独修理;②由乙单独修理;③甲、乙合作同时修理.你选哪种方案,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅游景点2015年六月份共接待游客25万人次,八月份共接待游客64万人次,设六至八月每月游客人次的平均增长率为x,则可列方程为( )
A.25(1+x)2=64
B.25(1﹣x)2=64
C.64(1+x)2=25
D.64(1﹣x)2=25
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com