
如图1,抛物线 平移后过点A(8,,0)和原点,顶点为B,对称轴与
平移后过点A(8,,0)和原点,顶点为B,对称轴与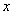 轴相交于点C,与原抛物线相交于点D.
轴相交于点C,与原抛物线相交于点D.
(1)求平移后抛物线的解析式并直接写出阴影部分的面积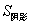 ;
;
(2)如图2,直线AB与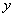 轴相交于点P,点M为线段OA上一动点,
轴相交于点P,点M为线段OA上一动点, 为直角,边MN与AP相交于点N,设
为直角,边MN与AP相交于点N,设 ,试探求:
,试探求:
① 为何值时
为何值时 为等腰三角形;
为等腰三角形;
② 为何值时线段PN的长度最小,最小长度是多少.
为何值时线段PN的长度最小,最小长度是多少.
【解析】(1)设平移后抛物线的解析式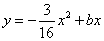 ,
,
将点A(8,,0)代入,得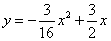 .顶点B(4,3),
.顶点B(4,3),
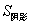 =OC×CB=12.
=OC×CB=12.
(2)直线AB的解析式为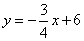 ,作NQ垂直于x轴于点Q,
,作NQ垂直于x轴于点Q,
①当MN=AN时, N点的横坐标为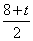 ,纵坐标为
,纵坐标为 ,
,
由三角形NQM和三角形MOP相似可知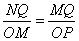 ,得
,得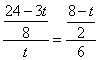 ,解得
,解得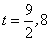 (舍去).
(舍去).
当AM=AN时,AN=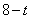 ,由三角形ANQ和三角形APO相似可知
,由三角形ANQ和三角形APO相似可知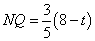
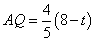 ,
,
MQ=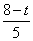 ,由三角形NQM和三角形MOP相似可知
,由三角形NQM和三角形MOP相似可知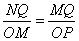 得:
得: ,解得:
,解得:
 =12(舍去).
=12(舍去).
当MN=MA时, 故
故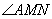 是钝角,显然不成立.
是钝角,显然不成立.
故 .
.
②方法一:作PN的中点C,连接CM,则CM=PC=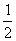 PN,
PN,
当CM垂直于x轴且M为OQ中点时PN最小,
此时 =3,证明如下:
=3,证明如下:
假设 =3时M记为
=3时M记为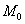 ,C记为
,C记为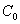
若M不在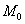 处,即M在
处,即M在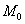 左侧或右侧,
左侧或右侧,
若C在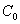 左侧或者C在
左侧或者C在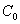 处,则CM一定大于
处,则CM一定大于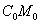 ,而PC却小于
,而PC却小于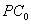 ,这与CM=PC矛盾,
,这与CM=PC矛盾,
故C在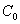 右侧,则PC大于
右侧,则PC大于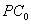 ,相应PN也会增大,
,相应PN也会增大,
故若M不在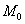 处时 PN大于
处时 PN大于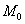 处的PN的值,
处的PN的值,
故当 =3时,MQ=3,
=3时,MQ=3, 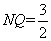 ,根据勾股定理可求出PM=
,根据勾股定理可求出PM=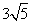 与MN=
与MN=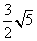 ,
,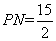 .
.
故当 =3时,PN取最小值为
=3时,PN取最小值为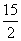 .
.
方法二:由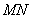 所在直线方程为
所在直线方程为 ,与直线AB的解析式
,与直线AB的解析式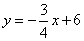 联立,
联立,
得点N的横坐标为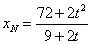 ,即
,即 ,
,
由判别式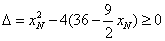 ,得
,得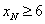 或
或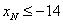 ,又
,又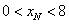 ,
,
所以 的最小值为6,此时
的最小值为6,此时 =3,
=3,
当 =3时,N的坐标为(6,
=3时,N的坐标为(6,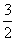 ),此时PN取最小值为
),此时PN取最小值为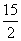 .
.


科目:初中数学 来源: 题型:
在一个不透明的口袋中,装有若干个出颜色不同其余都相同的球.如果口袋中装有3个红球且摸到红球的概率为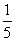 ,那么口袋中球的总个数为_
,那么口袋中球的总个数为_ ___________.
___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
一个不透明的袋子中有2个白球,3个黄球和1个红球,这些球除颜色不同外其他完全相同,则从袋子中随机摸出一个球是白球的概率为( )
A.  B.
B.  C.
C.  D.
D. 


查看答案和解析>>
科目:初中数学 来源: 题型:
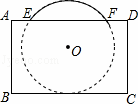
把球放在长方体纸盒内,球的一部分露出盒外,其主视图如图.⊙O与矩形ABCD的边BC,AD分别相切和相交(E,F是交点),已知EF=CD=8,则⊙O的半径为 .


查看答案和解析>>
科目:初中数学 来源: 题型:
下列事件中,必然事件是
A. 抛掷一枚硬币,正面朝上
B. 打开电视,正在播放广告
C. 体育课上,小刚跑完1000米所用时间为1分钟
D. 袋中只有4个球,且都是红球,任意摸出一球是红球


查看答案和解析>>
科目:初中数学 来源: 题型:
已知二次函数y=kx2+(2k﹣1)x﹣1与x轴交点的横坐标为x1,x2(x1<x2),则对于下列结论:
①当x=﹣2时,y=1;
②方程kx2+(2k﹣1)x﹣1=0有两个不相等的实数根x1,x2;
③x2﹣x1=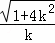 .
.
其中正确的结论有 (只需填写序号即可).


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com