
【题目】“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为( ) 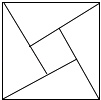
A.3
B.4
C.5
D.6
 新课标同步训练系列答案
新课标同步训练系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标中,菱形OABC的面积为12,点B在y轴上,点C在反比例函数y= ![]() 的图象上,则k的值为( )
的图象上,则k的值为( ) 
A.3
B.﹣3
C.6
D.﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一动点从半径为2的⊙O上的A0点出发,沿着射线A0O方向运动到⊙O上的点A1处,再向左沿着与射线A1O夹角为60°的方向运动到⊙O上的点A2处;接着又从A2点出发,沿着射线A2O方向运动到⊙O上的点A3处,再向左沿着与射线A3O夹角为60°的方向运动到⊙O上的点A4处;…按此规律运动到点A2017处,则点A2017与点A0间的距离是( )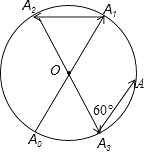
A.4
B.2 ![]()
C.2
D.0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,湿地景区岸边有三个观景台A、B、C,已知AB=1400米,AC=1000米,B点位于A点的南偏西60.7°方向,C点位于A点的南偏东66.1°方向.
(1)求△ABC的面积;
(2)景区规划在线段BC的中点D处修建一个湖心亭,并修建观景栈道AD,试求A、D间的距离.(结果精确到0.1米)
(参考数据:sin53.2°≈0.80,cos53.2°≈0.60,sin60.7°≈0.87,cos60.7°≈0.49,sin66.1°≈0.91,cos66.1°≈0.41, ![]() ≈1.414).
≈1.414).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=ax+b与双曲线y2= ![]() 交于A、B两点,与x轴交于点C,点A的纵坐标为6,点B的坐标为(﹣3,﹣2).
交于A、B两点,与x轴交于点C,点A的纵坐标为6,点B的坐标为(﹣3,﹣2). 
(1)求直线和双曲线的解析式;
(2)求点C的坐标,并结合图象直接写出y1<0时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,BC=2,∠BAC=30°,斜边AB的两个端点分别在相互垂直的射线OM、ON上滑动,下列结论:
①若C、O两点关于AB对称,则OA=2 ![]() ;
;
②C、O两点距离的最大值为4;
③若AB平分CO,则AB⊥CO;
④斜边AB的中点D运动路径的长为 ![]() ;
;
其中正确的是(把你认为正确结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB是⊙O的弦,点C是 ![]() 的中点,连接OB、OC,OC交AB于点D.
的中点,连接OB、OC,OC交AB于点D.
(1)如图1,求证:AD=BD; 
(2)如图2,过点B作⊙O的切线交OC的延长线于点M,点P是 ![]() 上一点,连接AP、BP,求证:∠APB﹣∠OMB=90°;
上一点,连接AP、BP,求证:∠APB﹣∠OMB=90°; 
(3)如图3,在(2)的条件下,连接DP、MP,延长MP交⊙O于点Q,若MQ=6DP,sin∠ABO= ![]() ,求
,求 ![]() 的值.
的值. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学活动课上小芳,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于 ![]() MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=8,AB=30,请你帮助她算一下△ABD的面积是( )
MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=8,AB=30,请你帮助她算一下△ABD的面积是( ) 
A.150
B.130
C.240
D.120
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com