
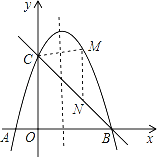
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,已知A(﹣1,0),C(0,3)
(1)求该抛物线的表达式;
(2)求BC的解析式;
(3)点M是对称轴右侧点B左侧的抛物线上一个动点,当点M运动到什么位置时,△BCM的面积最大?求△BCM面积的最大值及此时点M的坐标.

【答案】(1)抛物线的解析式y=-x2+2x+3;(2)BC的解析式为y=-x+3;(3)△BCM面积的最大值为![]() ,此时点M的坐标(
,此时点M的坐标(![]() ,
, ![]() ).
).
【解析】试题分析:
(1)将A、C坐标代入y=﹣x2+bx+c列方程组求得b、c的值即可求得解析式;
(2)由(1)中所求解析式可求得B的坐标,结合点C的坐标,用待定系数法可求得直线BC的解析式;
(3)过点M作MN∥y轴,交BC于点N,设点M的横坐标为“m”,则由(1)、(2)所得解析式可表达出M、N的纵坐标,从而可表达出MN的长度,在由S△BCM=![]() MN·OB即可用含“m”的式子表达出“S△BCM”,即可求得其最大值和此时点M的坐标.
MN·OB即可用含“m”的式子表达出“S△BCM”,即可求得其最大值和此时点M的坐标.
试题解析:
(1)将A、C点坐标代入函数解析式,得![]() ,
,
解得![]()
抛物线的解析式y=-x2+2x+3;
(2)当y=0时,有-x2+2x+3=0,解得:x1=-1,x2=3,
∴点B的坐标为:(3,0),
设直线BC的解析式为:y=kx+n,把B、C的坐标代入可得: ![]() 解得;
解得; ![]() ,∴直线BC的解析式为:y=-x+3;
,∴直线BC的解析式为:y=-x+3;
(3)如图,过点M作MN∥y轴,交BC于点N,
设点M的坐标为![]() ,则点N的坐标为
,则点N的坐标为![]() ,
,
又∵点M在点N的上方,
∴MN=![]() ,
,
∴S△BCM=![]() MN·OB
MN·OB
=![]()
= ![]()
=![]() .
.
∵点M是对称轴右侧、点B左侧的抛物线上一个动点,
∴![]() ,
,
∴当![]() 时,S△BCM最大=
时,S△BCM最大=![]() .此时点M的坐标为
.此时点M的坐标为![]() .
.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
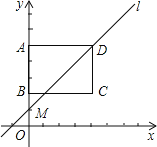
【题目】如图,在平面直角坐标系中,矩形ABCD的顶点A、B、C的坐标分别为(0,5)、(0,2)、(4,2),直线l的解析式为y=kx+5-4k(k>0).
(1)当直线l经过点B时,求一次函数的解析式;
(2)通过计算说明:不论k为何值,直线l总经过点D;
(3)直线l与y轴交于点M,点N是线段DM上的一点,且△NBD为等腰三角形,试探究:当函数y=kx+5-4k为正比例函数时,点N的个数有______个.
查看答案和解析>>
科目:初中数学 来源: 题型:
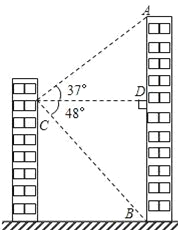
【题目】小明家所在居民楼的对面有一座大厦AB,AB=80米,为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.求小明家所在居民楼与大厦的距离CD的长度.(结果保留整数)
(参考数据: ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙C过原点O,且与两坐标轴分别交于点A、B,点A的坐标为(0,2),M是第三象限内⊙C上一点,∠BMO=120°,则圆心C的坐标为( )

A. (1,1) B. (1, ![]() ) C. (2,1) D. (﹣
) C. (2,1) D. (﹣![]() ,1)
,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,CA=CB=4,∠ACB=120°,点D在线段AB上运动(不与A、B重合),将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ.
(1)证明:CP=CQ;
(2)求∠PCQ的度数;
(3)当点D是AB中点时,请直接写出△PDQ是何种三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“综合与实践”学习活动准备制作一组三角形,记这些三角形分别为![]() ,用记号
,用记号![]() 表示一个满足条件的三角形,如(2,4,4)表示边长分别为2,4,4个单位长度的一个三角形.
表示一个满足条件的三角形,如(2,4,4)表示边长分别为2,4,4个单位长度的一个三角形.
(1)若这些三角形三边的长度为大于0且小于3的整数个单位长度,请用记号写出所有满足条件的三角形;
(2)如图,![]() 是
是![]() 的中线,线段
的中线,线段![]() 的长度分别为2个,6个单位长度,且线段
的长度分别为2个,6个单位长度,且线段![]() 的长度为整数个单位长度,过点
的长度为整数个单位长度,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.

①求![]() 的长度;
的长度;
②请直接用记号表示![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
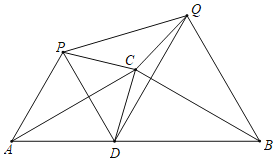
【题目】(1)如图 1,若 P是口ABCD 边 CD 上任意一点,连结 AP、BP,若△APB 的面积为 60 ,△APD 的面积为 18,则 S△APC= .
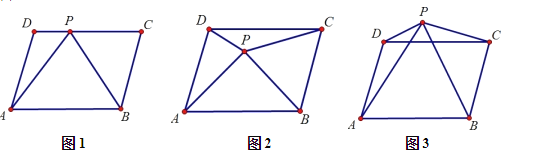
(2) 如图 2,①若点 P 运动到口ABCD 内一点时,试说明 S△APB +S△DPC =S△BPC +S△APD.
②若此时△APB 的面积为 60,△APD 的面积为 18,则 S△APC= .
(3)如图 3①利用(2)中的方法你会发现,S△APB ,S△DPC ,S△BPC ,S△APD 之间存在怎样的关系: .
②若此时△APB 的面积为 60,△APD 的面积为 18,请利用你的发现,求 S△APC 的面积?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有足够多除颜色外均相同的球,请你从中选![]() 个球设计摸球游戏.
个球设计摸球游戏.
(1)使摸到红球的概率和摸到白球的概率相等;
(2)使摸到红球、白球、黑球的概率都相等;
(3)使摸到红球的概率和摸到白球的概率相等,且都小于摸到黑球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在RtABC 中, BAC 90, AB AC ,点 D 是 AB 的中点,AF CD 于 H 交 BC 于 F, BE AC 交 AF 的延长线于 E.
求证:(1)ADC ≌ BEA
(2)BC 垂直平分 DE.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com