
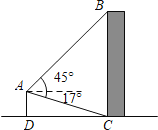
【题目】一夜之间,新冠病毒肺炎席卷全球。疫情期间,我国为保障大家的健康,各地采取了多种方式预防。其中,某地运用无人机规劝居民回家。如图,无人机于空中 A 处测得某建筑顶部 B 处的仰角为 45°,测得该建筑底部 C 处的俯角为 17°.若无人机的飞行高度 AD 为 62m,求该建筑的高度 BC .(参考数据:sin17°≈0.29,cos17°≈0.96,tan17°≈0.31)
科目:初中数学 来源: 题型:
【题目】如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为好玩三角形.若Rt△ABC是好玩三角形,且∠C=90°,BC≥AC,则sinB=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
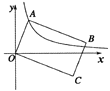
【题目】如图,已知点![]() 是反比例函数
是反比例函数![]() 在第一象限图像上的一个动点,连接
在第一象限图像上的一个动点,连接![]() ,以
,以![]() 为长,
为长,![]() 为宽作矩形
为宽作矩形![]() ,且点
,且点![]() 在第四象限,随着点
在第四象限,随着点![]() 的运动,点
的运动,点![]() 也随之运动,但点
也随之运动,但点![]() 始终在反比例函数
始终在反比例函数![]() 的图像上,则
的图像上,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
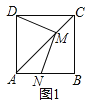
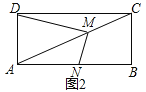
【题目】如图1,点M放在正方形ABCD的对角线AC(不与点A重合)上滑动,连结DM,做MN⊥DM,交直线AB于N.
(1)求证:DM=MN;
(2)若将(1)中的正方形变为矩形,其余条件不变如图,且DC=2AD,求MD:MN的值;
(3)在(2)中,若CD=nAD,当M滑动到CA的延长线上时(如图3),请你直接写出MD:MN的比值.
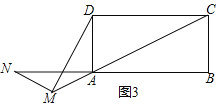
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形纸片ABCD边长为2,折叠∠B和∠D,使两个直角的顶点重合于对角线BD上的一点P,EF、GH分别是折痕(图2),设AE=x(0<x<2),给出下列判断:①x=![]() 时,EF+AB>AC;②六边形AEFCHG周长的值为定值;③六边形AEFCHG面积为定值,其中正确的是( )
时,EF+AB>AC;②六边形AEFCHG周长的值为定值;③六边形AEFCHG面积为定值,其中正确的是( )
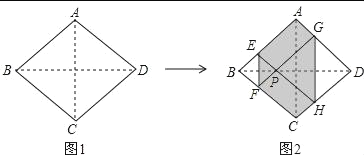
A.①②B.①③C.②D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线L:y=﹣![]() x+2与x轴、y轴分别交于A、B两点,在y轴上有一点N(0,4),动点M从A点以每秒1个单位的速度匀速沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,在y轴上有一点N(0,4),动点M从A点以每秒1个单位的速度匀速沿x轴向左移动.
(1)点A的坐标:_____;点B的坐标:_____;
(2)求△NOM的面积S与M的移动时间t之间的函数关系式;
(3)在y轴右边,当t为何值时,△NOM≌△AOB,求出此时点M的坐标;
(4)在(3)的条件下,若点G是线段ON上一点,连结MG,△MGN沿MG折叠,点N恰好落在x轴上的点H处,求点G的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°.
(1)判断CD与⊙O的位置关系,并说明理由;
(2)若⊙O半径为4cm,AE=6cm,求∠ADE的正切值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租公司有若干辆同一型号的货车对外出租,每辆货车的日租金实行淡季、旺季两种价格标准,旺季每辆货车的日租金比淡季上涨![]() .据统计,淡季该公司平均每天有
.据统计,淡季该公司平均每天有![]() 辆货车未出租,日租金总收入为
辆货车未出租,日租金总收入为![]() 元;旺季所有的货车每天能全部租出,日租金总收入为
元;旺季所有的货车每天能全部租出,日租金总收入为![]() 元.
元.
(1)该出租公司这批对外出租的货车共有多少辆?淡季每辆货车的日租金多少元?
(2)经市场调查发现,在旺季如果每辆货车的日租金每上涨![]() 元,每天租出去的货车就会减少
元,每天租出去的货车就会减少![]() 辆,不考虑其它因素,每辆货车的日租金上涨多少元时,该出租公司的日租金总收入最高?
辆,不考虑其它因素,每辆货车的日租金上涨多少元时,该出租公司的日租金总收入最高?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com