练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．在数-$\sqrt{2}$，0，1，$\sqrt{2}$中，最大的数是（　　）
    A．$\sqrt{2}$B．1C．0D．$-\sqrt{2}$

    分析 先将四个数分类，然后按照正数＞0＞负数的规则比较大小．

    解答 解；将-$\sqrt{2}$，0，1，$\sqrt{2}$四个数分类可知1、$\sqrt{2}$为正数，-$\sqrt{2}$为负数，且$\sqrt{2}$＞1，故最大的数为$\sqrt{2}$，
    故选：A．

    点评 此题主要考查了利用数轴比较实数的大小，解答此题的关键是熟知：数轴上的任意两个数，边的数总比左边的数大．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    7．如图，点O是矩形ABCD的中心，E是AB上的点，沿CE折叠后，点B恰好与点O重合，若BC=3，则折痕CE的长为（　　）
    A．$\sqrt{3}$B．2$\sqrt{3}$C．2D．3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

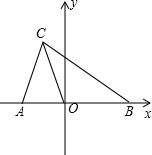    8．如图，在平面直角坐标系中，A（a，0），B（b，0），C（-1，3），且|$\frac{a}{2}$$+\frac{b}{3}$|+（4a-b+11）2=0．
    （1）求a、b的值；
    （2）①在y轴上的负半轴上存在一点M，使△COM的面积=$\frac{1}{2}$△ABC的面积，求出点M的坐标；
    ②在坐标轴的其它位置是否存在点M，使结论“△COM的面积=$\frac{1}{2}$△ABC的面积”仍然成立？若存在，请直接写出符合条件的点M的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．已知△ABC是等边三角形，D是BC边上的一个动点（点D不与B，C重合）△ADF是以AD为边的等边三角形，过点F作BC的平行线交射线AC于点E，连接BF．
    （1）如图1，求证：△AFB≌△ADC；
    （2）请判断图1中四边形BCEF的形状，并说明理由；
    （3）若D点在BC 边的延长线上，如图2，其它条件不变，请问（2）中结论还成立吗？如果成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．下列运算中，正确的是（　　）
    A．$\sqrt{-2}$×$\sqrt{-3}$=$\sqrt{（-2）×（-3）}$=$\sqrt{6}$B．2$\sqrt{3}$×3$\sqrt{2}$=6$\sqrt{6}$C．$\sqrt{{a}^{2}-4}$=$\sqrt{{a}^{2}}$-$\sqrt{4}$=a-2D．3$\sqrt{2}$+2$\sqrt{3}$=5$\sqrt{5}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

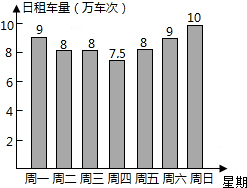    2．作为某市政府民生实事之一的公共自行车建设工作已基本完成，某部门对今年4月份中的7天进行了公共自行车日租车量的统计，结果如图：
    （1）求这7天日租车量的众数、中位数和平均数；
    （2）用（1）中的平均数估计4月份（30天）共租车多少万车次；
    （3）市政府在公共自行车建设项目中共投入9600万元，估计2015年共租车3200万车次，每车次平均收入租车费0.1元，求2015年租车费收入占总投入的百分率（精确到0.1%）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．在△ABC中，已知∠A=∠B=45°，BC=$\sqrt{2}$，则边AB的长为（　　）
    A．1B．$\sqrt{2}$C．2D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．任意画一个四边形，以四边的中点为顶点组成一个新四边形，这个新四边形的形状是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

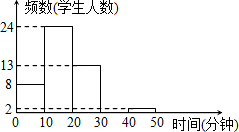    7．李老师为了了解本班学生作息时间，调查班上50名学生上学路上所花的时间，他发现学生所花时间都少于50min，然后将调查数据整理，作出如图15所示的频数直方图的一部分．
    （1）补全频数直方图；
    （2）该班学生在路上花费的时间在哪个范围内最多？
    （3）该班学生上学路上花费时间在30min以上（含30min）的人数占全班人数的百分比是多少？

    查看答案和解析>>

    同步练习册答案