
ЁОЬтФПЁПШчЭМ1,жБЯпABЗжБ№гыxжсЁЂyжсНЛгкAЁЂBСНЕу,OCЦНЗжЁЯAOBНЛABгкЕуC,ЕуDЮЊЯпЖЮABЩЯвЛЕу,Й§ЕуDзїDE//OCНЛyжсгкЕуE,вбжЊAO=m,BO=n,ЧвmЁЂnТњзуn2-12+36+|n-2m|=0.
(1)ЧѓAЁЂBСНЕуЕФзјБъ?
(2)ШєЕуDЮЊABжаЕу,ЧѓOEЕФГЄ?
(3)ШчЭМ2,ШєЕуP(x,-2x+6)ЮЊжБЯпABдкxжсЯТЗНЕФвЛЕу,ЕуEЪЧyжсЕФе§АыжсЩЯвЛЖЏЕу,вдEЮЊжБНЧЖЅЕузїЕШбќжБНЧЁїPEF,ЪЙЕуFдкЕквЛЯѓЯо,ЧвFЕуЕФКсЁЂзнзјБъЪМжеЯрЕШ,ЧѓЕуPЕФзјБъ.


ЁОД№АИЁП(1) ЕуAЮЊЃЈ3,0ЃЉЃЌЕуBЮЊЃЈ0,6ЃЉ;(2) OE=1.5;(3) ЕуPЮЊЃЈ6ЃЌ-6ЃЉ.
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉИљОнЗЧИКЪ§ЕФаджЪЃЌЕУГіЗНГЬЃЈn-6ЃЉ2=0ЃЌ|n-2m|=0ЃЌЧѓЕУm=3ЃЌn=6ЃЌМДПЩЕУЕНAЁЂBСНЕуЕФзјБъЃЛЃЈ2ЃЉбгГЄDEНЛxжсгкЕуFЃЌбгГЄFDЕНЕуGЃЌЪЙЕУDG=DFЃЌСЌНгBGЃЌЙЙдьШЋЕШШ§НЧаЮЃЌдйИљОнBG=BEСаГіЙигкxЕФЗНГЬЃЌМДПЩЧѓЕУOEЕФГЄЃЛЃЈ3ЃЉЗжБ№Й§ЕуFЁЂPзїFMЁЭyжсгкЕуMЃЌPNЁЭyжсгкЕуNЃЌЩшЕуEЮЊЃЈ0ЃЌmЃЉЃЌЙЙдьШЋЕШШ§НЧаЮЃЌдйИљОнFЕуЕФКсзјБъгызнзјБъЯрЕШЃЌЕУГіЗНГЬm+2x-6=m+xЃЌНтЕУЃКx=6ЃЌМДПЩЕУЕНЕуPЮЊЃЈ6ЃЌ-6ЃЉЃЎ
БОЬтНтЮіЃК
ЃЈ1ЃЉЁп![]()
Ёр![]()
Ёп![]() ЃЌ
ЃЌ ![]()
Ёр![]() ,
,![]()
Ёр m=3ЃЌn=6
ЁрЕуAЮЊЃЈ3,0ЃЉЃЌЕуBЮЊЃЈ0,6ЃЉ
ЃЈ2ЃЉбгГЄDEНЛxжсгкЕуFЃЌбгГЄFDЕНЕуGЃЌЪЙЕУDG=DFЃЌСЌНгBG
ЩшOE=x
ЁпOCЦНЗжЁЯAOB
ЁрЁЯBOC=ЁЯAOC=45Ёу
ЁпDEЁЮOC
ЁрЁЯEFO=ЁЯFEO=ЁЯBEG=ЁЯBOC=ЁЯAOC=45Ёу
ЁрOE=OF=x
дкЁїADFКЭЁїBDGжа
Ёп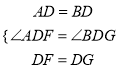
ЁрЁїADFЁеЁїBDGЃЈSASЃЉ
ЁрBG=AF=3+xЃЌЁЯG=ЁЯAFE=45Ёу
ЁрЁЯG=ЁЯBEG=45Ёу
ЁрBG=BE=6-x
Ёр6-x=3+x
НтЕУЃКx=1.5
ЁрOE=1.5
ЃЈ3ЃЉЗжБ№Й§ЕуFЁЂPзїFMЁЭyжсгкЕуMЃЌPNЁЭyжсгкЕуN
ЩшЕуEЮЊЃЈ0ЃЌmЃЉ
ЁпЕуPЕФзјБъЮЊЃЈxЃЌ-2x+6ЃЉ
дђPN=xЃЌEN=m+2x-6
ЁпЁЯPEF=90Ёу
ЁрЁЯPEN+ЁЯFEM=90Ёу
ЁпFMЁЭyжс
ЁрЁЯMFE+ЁЯFEM=90Ёу
ЁрЁЯPEN=ЁЯMFE
дкЁїEFMКЭЁїPENжа
Ёп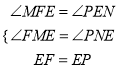
ЁрЁїEFMЁеЁїPENЃЈAASЃЉ
ЁрME=NP=xЃЌFM=EN=m+2x-6
ЁрЕуFЮЊЃЈm+2x-6ЃЌm+xЃЉ
ЁпFЕуЕФКсзјБъгызнзјБъЯрЕШ
Ёрm+2x-6=m+x
НтЕУЃКx=6
ЁрЕуPЮЊЃЈ6ЃЌ-6ЃЉ



 ПкЫуаФЫуЫйЫугІгУЬтЯЕСаД№АИ
ПкЫуаФЫуЫйЫугІгУЬтЯЕСаД№АИ ЭЌВНЭиеЙдФЖСЯЕСаД№АИ
ЭЌВНЭиеЙдФЖСЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌEЁЂFЪЧЖдНЧЯпBDЩЯСНЕуЃЌЧвЁЯEAF=45ЁуЃЌНЋЁїADFШЦЕуAЫГЪБеыа§зЊ90ЁуКѓЃЌЕУЕНЁїABQЃЌСЌНгEQЃЌЧѓжЄЃК
ЃЈ1ЃЉEAЪЧЁЯQEDЕФЦНЗжЯпЃЛ
ЃЈ2ЃЉEF2=BE2+DF2ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаИїЪНжаВЛФмгУЦНЗНВюЙЋЪНМЦЫуЕФЪЧЃЈ ЃЉ
A.ЃЈxЉyЃЉЃЈЉx+yЃЉ
B.ЃЈЉx+yЃЉЃЈЉxЉyЃЉ
C.ЃЈЉxЉyЃЉЃЈxЉyЃЉ
D.ЃЈx+yЃЉЃЈЉx+yЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌAB//CD,ЁЯA=100Ёу,ЁЯC=75Ёу,ЁЯ1:ЁЯ2=5:7,ЧѓЁЯBЕФЖШЪ§.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМ1ЃЌНЋСНПщШЋЕШЕФКЌ30НЧЕФжБНЧШ§НЧАхАДЭМЫљЪОЕФЗНЪНЗХжУЃЌЁЯBAC=ЁЯB1A1C=30ЁуЃЌЕуBЃЌCЃЌB1дкЭЌвЛЬѕжБЯпЩЯЃЎ
ЃЈ1ЃЉЧѓжЄЃКAB=2BC
ЃЈ2ЃЉШчЭМЃВЃЌНЋЁїABCШЦЕуЃУЫГЪБеыа§зЊІСЁуЃЈ0ЃМІСЃМ180ЃЉЃЌдка§зЊЙ§ГЬжаЃЌЩшABгыA1CЁЂA1B1ЗжБ№НЛгкЕуDЁЂEЃЌACгыA1B1НЛгкЕуFЃЎЕБІСЕШгкЖрЩйЖШЪБЃЌABгыA1B1ДЙжБЃПЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШчЭМ3ЃЌЕБЁїABCШЦЕуCЫГЪБеыЗНЯђа§зЊжСШчЭМЫљЪОЕФЮЛжУЃЌЪЙABЁЮCB1ЃЌABгыA1CНЛгкЕуDЃЌЪдЫЕУїA1D=CD.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЕуPЃЈЉ2ЃЌ1ЃЉдкЕк ________ЯѓЯоЃЎЙигкxжсЕФЖдГЦЕузјБъЮЊ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋЯТСаЖрЯюЪНЗжНтвђЪНЃЌНсЙћжаВЛКЌвђЪНxЉ1ЕФЪЧЃЈ ЃЉ
A.x2Љ1
B.xЃЈxЉ2ЃЉ+ЃЈ2ЉxЃЉ
C.x2Љ2x+1
D.x2+2x+1
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЖрБпаЮжаЃЌФкНЧКЭЪЧЭтНЧКЭЕФСНБЖЕФЪЧЃЈ ЃЉ
A.ЫФБпаЮ
B.ЮхБпаЮ
C.СљБпаЮ
D.АЫБпаЮ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com