
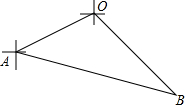
 如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东30°方向以每小时10海里的速度航行,甲沿南偏西75°方向以每小时10$\sqrt{2}$海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.则甲船追赶乙船的速度为10+10$\sqrt{3}$海里/小时?
如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东30°方向以每小时10海里的速度航行,甲沿南偏西75°方向以每小时10$\sqrt{2}$海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.则甲船追赶乙船的速度为10+10$\sqrt{3}$海里/小时? 分析 根据题意画图,过O向AB作垂线,根据特殊角的三角函数值求得AC、BC的值,从而求得AB的值.根据追及问题的求法求甲船追赶乙船的速度.
解答 解:如图:乙沿南偏东30°方向航行则∠DOB=30°,甲沿南偏西75°方向航行,则∠AOD=75°,
当航行1小时后甲沿南偏东60°方向追赶乙船,则∠2=90°-60°=30°.
∵∠3=∠AOD=75°,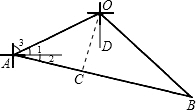
∴∠1=90°-75°=15°,
故∠1+∠2=15°+30°=45°.
过O向AB作垂线,则∠AOC=90°-∠1-∠2=90°-15°-30°=45°,
∵OA=10 $\sqrt{3}$,∠OAB=∠AOC=45°,
∴OC=AC=OA•sin45°=10 $\sqrt{2}$×$\frac{\sqrt{2}}{2}$=10.
在Rt△OBC中,∠BOC=∠AOD+∠BOD-∠AOC=75°+30°-45°=60°,
∴BC=OC•tan60°=10 $\sqrt{3}$,
∴AB=AC+BC=10+10 $\sqrt{3}$.
因为OC=10海里,∠B=30°,所以OB=2OC=2×10=20,
乙船从O到B所用时间为20÷10=2小时,
由于甲从O到A所用时间为1小时,则从A到B所用时间为2-1=1小时,
甲船追赶乙船的速度为10+10 $\sqrt{3}$海里/小时.
点评 本题考查解直角三角形-方向角问题、勾股定理等知识,结合航海中的实际问题,转化为解直角三角形的相关知识,体现了数学应用于实际生活的思想.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
| 车型 | 载货能力(箱/辆) | 运费 | |
| 甲村(元/辆) | 乙村(元/辆) | ||
| 大货车 | 70 | 800 | 900 |
| 小货车 | 35 | 400 | 600 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上),网格中小正方形的边长为1.
如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上),网格中小正方形的边长为1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
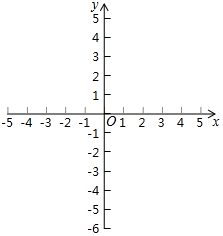 抛物线F与x轴相交于A、B两点(点A在点B的左边),对称轴为直线x=1,顶点C在直线y=x-5上,与y轴相交于点D(0,3).
抛物线F与x轴相交于A、B两点(点A在点B的左边),对称轴为直线x=1,顶点C在直线y=x-5上,与y轴相交于点D(0,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com