【题目】如图是甲、乙两人同一地点出发后，路程随时间变化的图象．
（1）两个变量中， 是自变量， 是因变量；
（2）甲的速度 乙的速度（填<、=、或>）；
（3）路程为150km时，甲行驶了 小时，乙行驶了 小时．
（4）甲比乙先走了 小时；在9时， 走在前面。
【答案】见解析
【解析】试题分析：（1）根据自变量与因变量的含义得到时间是自变量，路程是因变量；
（2）甲走6行驶100千米，乙走3小时行驶了100千米，则可得到它们的速度的大小；
（3）观察图象得到路程为150km，甲行驶9小时；乙行驶了7-3=4小时；
（4）观察图象得到甲先出发3小时后，乙才开始出发．观察图象得到t=9时，乙的图象在甲的上方，即乙行驶的路程远些.
试题解析：（1）两个变量中， 时间 是自变量， 路程 是因变量.
（2）甲的速度 < 乙的速度．（<、=、>）
（3）路程为150km，甲行驶了 9 小时，乙行驶了 4 小时．
（4）甲比乙先走了 3 小时，在9时 乙 走在前面.
科目：初中数学 来源： 题型：
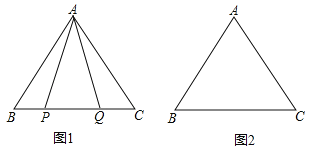
【题目】在等边△ABC中：
（1）如图1，P，Q是BC边上的两点，AP=AQ，∠BAP=20°，求∠AQB的度数；
（2）点P，Q是BC边上的两个动点（不与点B，C重合），点P在点Q的左侧，且AP=AQ，点Q关于直线AC的对称点为M，连接AM，PM．
①依题意将图2补全；
②小茹通过观察、实验提出猜想：在点P，Q运动的过程中，始终有PA=PM，小茹把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：
想法1：要证明PA=PM，只需证△APM是等边三角形；
想法2：在BA上取一点N，使得BN=BP，要证明PA=PM，只需证△ANP≌△PCM；
想法3：将线段BP绕点B顺时针旋转60°，得到线段BK，要证PA=PM，只需证PA=CK，PM=CK…
请你参考上面的想法，帮助小茹证明PA=PM（一种方法即可）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场要经营一种新上市的文具，进价为20元/件。试营销阶段发现:当销售单价25元/件时，每天的销售量是250件；销售单价每上涨1元，每天的销售量就减少10件。
(1)写出商场销售这种文具，每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式。
(2)求销售单价为多少元时，该文具每天的销售利润最大?
(3)商场的营销部结合上述情况，提出了A,B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元；
方案B:每天销售量不少于10件，且每件文具的利润至少为25元。
请比较哪种方案的最大利润更高，并说明理由。（本题12分）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】请你做评委：在一堂数学活动课上，同在一合作学习小组的小明、小亮、小丁、小彭对刚学过的知识发表了自己的一些感受：
小明说：“绝对值不大于4的整数有7个．”
小丁说：“若|a|=3，|b|=2，则a+b的值为5或1．”
小亮说：“﹣ 
＜﹣
，因为两个负数比较大小，绝对值大的数反而小．”
小彭说：“代数式a2+b2表示的意义是a与b的和的平方”
依次判断四位同学的说法是否正确，如不正确，请帮他们修正，写出正确的说法．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABD和△ACE中，有下列判断：
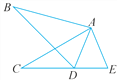
①AB＝AC；②∠B＝∠C；③∠BAC＝∠EAD；④AD＝AE.
请用其中的三个判断作为条件，余下的一个判断作为结论(用序号的形式)，写出一个由三个条件能推出结论成立的式子，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
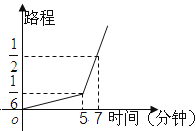
【题目】一名考生步行前往考场，5分钟走了总路程的
，估计步行不能准时到达，于是他改乘出租车赶往考场，他的行程与时间关系如图所示（假定总路程为1，出租车匀速），则他到达考场所花的时间比一直步行提前了________分钟。
查看答案和解析>>
科目：初中数学 来源： 题型：
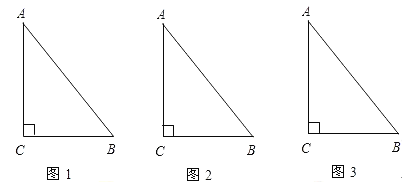
【题目】某园艺公司对一块直角三角形的花圃进行改造．测得两直角边长为6m、8m．现要将其扩建成等腰三角形，且扩充部分是以8m为直角边的直角三角形．求扩建后的等腰三角形花圃的周长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
