
如图,△ABC是等边三角形,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F.若BC=2,则DE+DF=( )

A. 1 B. 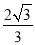 C.
C. 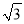 D.
D. 
科目:初中数学 来源:广东省东莞市翰林学校2017-2018学年八年级(上)期中数学试卷(word版含答案解析) 题型:单选题
在平面直角坐标系中,点P(﹣1,2)的位置在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
B 【解析】 试题分析:本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点.四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).∵点P(﹣1,2)的横坐标﹣1<0,纵坐标2>0,∴点P在第二象限.查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十九章达标检测卷 题型:填空题
如果一次函数y=(k﹣2)x+1的图象经过一、二、三象限,那么常数k的取值范围是______.
k>2; 【解析】根据一次函数图像与性质,可知图像过一、二、三象限时,k-2>0,解得k>2. 故答案为:k>2.查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:解答题
如图,某塔观光层的最外沿点E为蹦极项目的起跳点,已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到1米,参考数据 ≈1.4,
≈1.4, 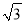 ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:填空题
如图,正方形ABCD的边长为4,点M在边DC上,M,N两点关于对角线AC对称,若DM=1,则tan∠ADN=________.

查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:单选题
如图,要测量河两岸A,C两点间的距离,已知AC⊥AB,测得AB=a,∠ABC=α,那么AC等于( )

A. a·sin α B. a·cos α C. a·tan α D. 
查看答案和解析>>
科目:初中数学 来源:河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
ABN和△ACM的位置如图所示,AB=AC,AD=AE,∠1=∠2.
求证:(1)BD=CE;(2)∠M=∠N.

查看答案和解析>>
科目:初中数学 来源:河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
下列图形中,不是轴对称图形的是()
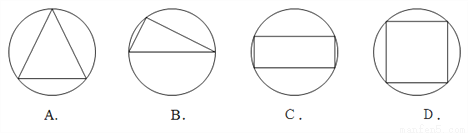
A. (A) B. (B) C. (C) D. (D)
B 【解析】A、 是轴对称图形,故本选项错误; B、不是轴对称图形,故本选项正确; C、是轴对称图形,故本选项错误; D、是轴对称图形,故本选项错误. 故选B.查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2018届九年级上学期期末考试数学试卷 题型:填空题
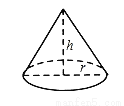
如图,圆锥的底面半径r为6cm,高h为8cm,则圆锥的侧面积为______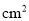 .(结果保留
.(结果保留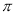 ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com