
【题目】C,D两城蔬菜紧缺,A,B两城决定支援,A城有蔬菜20吨,B城有蔬菜40吨,C城需要蔬菜16吨,D城需要蔬菜44吨,已知A到C,D的运输费用分别为200元/吨,220元/吨,B到C,D的运输费用分别为300元/吨,340元/吨,规定A向C城运的吨数不小于B向C城运的吨数,设A城向C城运x吨,请回答下列问题:
(1)根据题意条件,填写下列表格:

(2)设总费用为y(元),求出y(元)与x(吨)的函数关系式,并写出x的取值范围;
(3)怎样调运货物能使总费用最少?最少费用是多少?
【答案】(1)①![]() ,②
,②![]() ,③
,③![]() ;(2)
;(2)![]() ,
,![]() ;(3)当A向C城运8吨,向D城运12吨,B向C城运8吨,向D城运32吨时费用最少,最少费用是17520元.
;(3)当A向C城运8吨,向D城运12吨,B向C城运8吨,向D城运32吨时费用最少,最少费用是17520元.
【解析】
(1)用C城需要蔬菜的吨数减去x可得①的值;用A城共有的蔬菜吨数减去x可得②的值;用B城共有的蔬菜吨数减去①的值可得③的值;
(2)在(1)的基础上,根据题干已知的运输费用列出等式即可得;再根据“A向C城运的吨数不小于B向C城运的吨数”以及①、②的值均为非负数即可得求出x的取值范围;
(3)根据(2)的结论,利用一次函数的性质即可得.
(1)由题意得:①的值为![]() ;②的值为
;②的值为![]() ;③的值为
;③的值为![]()
故答案为:![]() ,
,![]() ,
,![]() ;
;
(2)由题意得:![]()
整理得:![]()
![]() ①、②的值均为非负数
①、②的值均为非负数
![]()
解得![]()
又![]() A向C城运的吨数不小于B向C城运的吨数
A向C城运的吨数不小于B向C城运的吨数
![]()
解得![]()
综上,x的取值范围是![]() ;
;
(3)由(2)知,![]() ,且
,且![]()
由一次函数的性质可知,当![]() 时,y随x的增大而增大
时,y随x的增大而增大
则当![]() 时,y取得最小值,最小值为
时,y取得最小值,最小值为![]() (元)
(元)
此时,![]() ,
,![]() ,
,![]()
答:当A向C城运8吨,向D城运12吨,B向C城运8吨,向D城运32吨时费用最少,最少费用是17520元.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.
(1)证明:四边形CDEF是平行四边形;
(2)若四边形CDEF的周长是16cm,AC的长为8cm,求线段AB的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了了解七年级男生入学时的跳绳情况,随机选取50名刚入学的男生进行个人一分钟跳绳测试,并以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图(如图所示).根据图表解答下列问题:
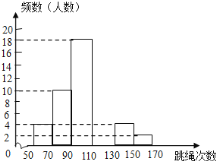
(1)a= ,b= ;
(2)这个样本数据的中位数落在第 组;
(3)若七年级男生个人一分钟跳绳次数x≥130时成绩为优秀,则从这50名男生中任意选一人,跳绳成绩为优秀的概率为多少;
(4)若该校七年级入学时男生共有150人,请估计此时该校七年级男生个人一分钟跳绳成绩为优秀的人数.
组别 | 次数x | 频数(人数) |
第1组 | 50≤x<70 | 4 |
第2组 | 70≤x<90 | a |
第3组 | 90≤x<110 | 18 |
第4组 | 110≤x<130 | b |
第5组 | 130≤x<150 | 4 |
第6组 | 150≤x<170 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请完成下列的相似测试.
如图,在△ABC中,AB=AC=4,D是AB上一点,且BD=1,连接CD,然后作∠CDE=∠B,交平行于BC且过点A的直线于点E,DE交AC于点F,连接CE.
(1)求证:△AFD∽△EFC;
(2)试求AEBC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:


(1)请将右上表补充完整:(参考公式:方差![]() )
)
(2)请从下列三个不同的角度对这次测试结果进行①从平均数和方差相结合看,__________的成绩好些;②从平均数和中位数相结合看,___________的成绩好些;
(3)若其他队选手最好成绩在9环左右,现要选一人参赛,你认为选谁参加,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号中:8,﹣![]() ,+2.8,π,
,+2.8,π,![]() ,﹣0.003,0,﹣100,﹣3.626626662……
,﹣0.003,0,﹣100,﹣3.626626662……
正数集合{_____ …}
整数集合{_____…}
负分数集合{_____ …}
无理数集合{_____ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )

A. 36=15+21 B. 25=9+16 C. 13=3+10 D. 49=18+31
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABE中,点A、B是反比例函数y=![]() (k≠0)图象上的两点,点E在x轴上,延长线段AB交y轴于点C,点B恰为线段AC中点,过点A作AD⊥x轴于点D.若S△ABE=
(k≠0)图象上的两点,点E在x轴上,延长线段AB交y轴于点C,点B恰为线段AC中点,过点A作AD⊥x轴于点D.若S△ABE=![]() ,DE=2OE,则k的值为( )
,DE=2OE,则k的值为( )
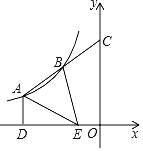
A.6B.﹣6C.9D.﹣9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:大数学家高斯在上学读书时曾经研究过这样一个问题:1+2+3+…+100=?经过研究,这个问题的一般性结论是1+2+3+…+n=![]() n(n+1),其中n是正整数.现在我们来研究一个类似的问题:1×2+2×3+…n(n+1)=?
n(n+1),其中n是正整数.现在我们来研究一个类似的问题:1×2+2×3+…n(n+1)=?
观察下面三个特殊的等式:
1×2=![]() (1×2×3﹣0×1×2)
(1×2×3﹣0×1×2)
2×3=![]() (2×3×4﹣1×2×3)
(2×3×4﹣1×2×3)
3×4=![]() (3×4×5﹣2×3×4)
(3×4×5﹣2×3×4)
将这三个等式的两边相加,可以得到1×2+2×3+3×4=![]() ×3×4×5=20,
×3×4×5=20,
读完这段材料,请你思考后回答:
(1)1×2+2×3+…+10×11=________________;
(2)1×2+2×3+3×4+…+n×(n+1)=_________________________;
(3)1×2×3+2×3×4+…+n(n+1)(n+2)=______________________________.
(只需写出结果,不必写中间的过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com