
 如图,在直角三角形ABC中,∠ACB=90°,CA=4.点P是半圆弧AC的中点,连接BP,线段BP把图形APCB(指半圆和直角三角形ABC组成的图形)分成两部分,则这两部分面积之差的绝对值是( )
如图,在直角三角形ABC中,∠ACB=90°,CA=4.点P是半圆弧AC的中点,连接BP,线段BP把图形APCB(指半圆和直角三角形ABC组成的图形)分成两部分,则这两部分面积之差的绝对值是( )| A. | 2 | B. | 4 | C. | 1.5π-2 | D. | $\frac{2π}{3}$ |
分析 连接OP、OB,把两部分的面积均可转化为规则图形的面积,不难发现两部分面积之差的绝对值即为三角形BOP的面积的2倍.
解答 解:连接OP、OB,如图所示: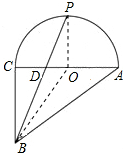
∵图形BAP的面积=△AOB的面积+△BOP的面积+扇形OAP的面积,
图形BCP的面积=△BOC的面积+扇形OCP的面积-△BOP的面积,
又∵点P是半圆弧AC的中点,OA=OC,
∴扇形OAP的面积=扇形OCP的面积,△AOB的面积=△BOC的面积,
∴两部分面积之差的绝对值是2S△BOP=OP•OC=4;
故选:B.
点评 本题考查了扇形面积的计算、三角形面积的计算;此题要能够把不规则图形的面积转化为规则图形的面积.注意根据已知条件发现面积相等的图形.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | -4≤a<-3 | B. | -4<a≤-3 | C. | -5≤a<-4 | D. | -5<a≤-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
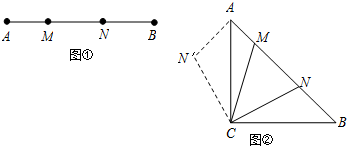
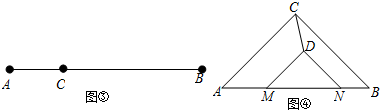
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com