
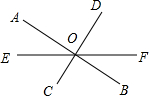
 如图,直线AB与CD相交于点O,若∠AOD=70°,∠BOE-∠BOC=50°,求∠DOE的度数.
如图,直线AB与CD相交于点O,若∠AOD=70°,∠BOE-∠BOC=50°,求∠DOE的度数. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在△ODC中,∠D=90°,CE是∠DCO的角平分线,且OE⊥CE,过点E作EF⊥OC于点F,猜想:线段EF与OD之间的数量关系,并证明.
已知:如图,在△ODC中,∠D=90°,CE是∠DCO的角平分线,且OE⊥CE,过点E作EF⊥OC于点F,猜想:线段EF与OD之间的数量关系,并证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,已知BD、CE是△ABC的两条高,过点D的直线交BC和BA的延长线于G、H,交CE于F,且∠H=∠BCF,求证:GD2=GF•GH.
如图所示,已知BD、CE是△ABC的两条高,过点D的直线交BC和BA的延长线于G、H,交CE于F,且∠H=∠BCF,求证:GD2=GF•GH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某水果批发市场新进一批水果,有苹果、西瓜、桃子和香蕉四个品种,统计后将结果绘制成条形图(如图),已知西瓜的重量占这批水果总重量的40%.
某水果批发市场新进一批水果,有苹果、西瓜、桃子和香蕉四个品种,统计后将结果绘制成条形图(如图),已知西瓜的重量占这批水果总重量的40%.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 阅读下面材料:
阅读下面材料:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com