
【题目】如图1,A、B两点在数轴上对应的数分别为﹣12和4.
(1)直接写出A、B两点之间的距离;
(2)若在数轴上存在一点P,使得AP=![]() PB,求点P表示的数.
PB,求点P表示的数.

(3)如图2,现有动点P、Q,若点P从点A出发,以每秒5个单位长度的速度沿数轴向右运动,同时点Q从点B出发,以每秒2个单位长度的速度沿数轴向左运动,当点Q到达原点O后立即以每秒3个单位长度的速度沿数轴向右运动,求:当OP=4OQ时的运动时间t的值.

【答案】(1)A、B两点之间的距离是16;(2)点P表示的数为﹣8或﹣20;(3)当OP=4OQ时的运动时间t的值为![]() 或
或![]() 秒.
秒.
【解析】
(1)根据两点间的距离公式即可求出A、B两点之间的距离;
(2)设点P表示的数为x.分两种情况:①点P在线段AB上;②点P在线段BA的延长线上.根据AP=![]() PB列出关于x的方程,求解即可;
PB列出关于x的方程,求解即可;
(3)根据点Q的运动方向分两种情况:①当t≤2时,点Q从点B出发,以每秒2个单位长度的速度沿数轴向左运动;②当t>2时,点Q从原点O开始以每秒3个单位长度的速度沿数轴向右运动,根据OP=4OQ列出关于t的方程,解方程即可.
(1)A、B两点之间的距离是:4﹣(﹣12)=16.
(2)设点P表示的数为x.分两种情况:
①当点P在线段AB上时,
∵AP=![]() PB,
PB,
∴x+12=![]() (4﹣x),
(4﹣x),
解得x=﹣8;
②当点P在线段BA的延长线上时,
∵AP=![]() PB,
PB,
∴﹣12﹣x=![]() (4﹣x),
(4﹣x),
解得x=﹣20.
综上所述,点P表示的数为﹣8或﹣20;
(3)分两种情况:
①当t≤2时,点Q从点B出发,以每秒2个单位长度的速度沿数轴向左运动,
此时Q点表示的数为4﹣2t,P点表示的数为﹣12+5t,
∵OP=4OQ,
∴12﹣5t=4(4﹣2t),
解得t=![]() ,符合题意;
,符合题意;
②当t>2时,点Q从原点O开始以每秒3个单位长度的速度沿数轴向右运动,
此时Q点表示的数为3(t﹣2),P点表示的数为﹣12+5t,
∵OP=4OQ,
∴|12﹣5t|=4×3(t﹣2),
∴12﹣5t=12t﹣24,或5t﹣12=12t﹣24,
解得t=![]() ,符合题意;或t=
,符合题意;或t=![]() ,不符合题意舍去.
,不符合题意舍去.
综上所述,当OP=4OQ时的运动时间t的值为![]() 或
或![]() 秒.
秒.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,一个长5m的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为4m,如果梯子的顶端A沿墙下滑1m至C点.
(1)求梯子底端B外移距离BD的长度;
(2)猜想CE与BE的大小关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有两点A、B,点A对应的数是40,点B对应的数是![]() .
.
![]() 求线段AB的长.
求线段AB的长.
![]() 如图2,O表示原点,动点P、T分别从B、O两点同时出发向左运动,同时动点Q从点A出发向右运动,点P、T、Q的速度分别为5个单位长度
如图2,O表示原点,动点P、T分别从B、O两点同时出发向左运动,同时动点Q从点A出发向右运动,点P、T、Q的速度分别为5个单位长度![]() 秒、1个单位长度
秒、1个单位长度![]() 秒、2个单位长度
秒、2个单位长度![]() 秒,设运动时间为t.
秒,设运动时间为t.
![]() 求点P、T、Q表示的数
求点P、T、Q表示的数![]() 用含有t的代数式表示
用含有t的代数式表示![]() ;
;
![]() 在运动过程中,如果点M为线段PT的中点,点N为线段OQ的中点,试说明在运动过程中等量关系
在运动过程中,如果点M为线段PT的中点,点N为线段OQ的中点,试说明在运动过程中等量关系![]() 始终成立.
始终成立.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,我市居民使用自来水计费方式实施阶梯水价,具体标准见表1,表2分别是小明、小丽、小斌、小宇四家2017年的年用水量和缴纳水费情况.
表1:大连市居民自来水实施阶梯水价标准情况:
阶梯 | 每户年用水量(立方米) | 水价(含污水处理费)(元/立方米) |
第一阶梯 | 0~m(含m) | a |
第二阶梯 | m~240(含240) | 4.40 |
第三阶梯 | 240以上 | 7.85 |
表2:四个家庭2017年的年用水量和缴纳水费情况:
家庭 | 小明 | 小丽 | 小斌 | 小宇 |
用水量(立方米) | 50 | 100 | 200 | 220 |
水费(元) | 162.5 | 325 | 673 | 761 |
请你根据表1、表2提供的数据回答下列问题:
(1)写出表1中的a,m的值;
(2)小颖家2017年使用自来水共缴纳水费827元,则她家2017年的年用水量是多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李在某商场购买![]() 两种商品若干次(每次
两种商品若干次(每次![]() 商品都买) ,其中前两次均按标价购买,第三次购买时,
商品都买) ,其中前两次均按标价购买,第三次购买时,![]() 商品同时打折.三次购买
商品同时打折.三次购买![]() 商品的数量和费用如下表所示:
商品的数量和费用如下表所示:
购买A商品的数量/个 | 购买B商品的数量/个 | 购买总费用/元 | |
第一次 |
|
|
|
第二次 |
|
|
|
第三次 |
|
|
|
(1)求![]() 商品的标价各是多少元?
商品的标价各是多少元?
(2)若小李第三次购买时![]() 商品的折扣相同,则商场是打几折出售这两种商品的?
商品的折扣相同,则商场是打几折出售这两种商品的?
(3)在(2)的条件下,若小李第四次购买![]() 商品共花去了
商品共花去了![]() 元,则小李的购买方案可能有哪几种?
元,则小李的购买方案可能有哪几种?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°,求∠B的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由相同的花盆按一定的规律组成的形如正多边形的图案,其中第1个图形共有6个花盆,第2个图形一共有12个花盆,第3个图形一共有20个花盆,…,则第10个图形中花盆的个数为( )

A. 110B. 120C. 132D. 140
查看答案和解析>>
科目:初中数学 来源: 题型:
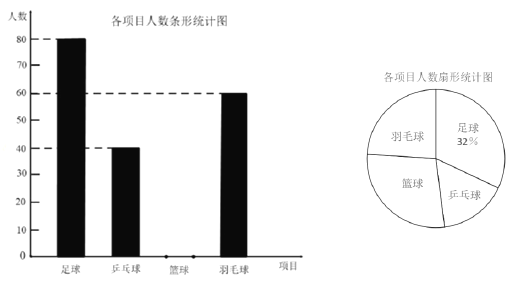
【题目】某学校举行“每天锻炼一小时,健康生活一辈子”为主题的体育活动,并开展了以下体育项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项。为了解选择各项体育活动的学生人数,随机抽取了部分学生进行调查,并将获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题:
(1)这次活动一共调查了 名学生;
(2)补全条形统计图;
(3)求选择篮球项目的人数在扇形统计图中所占的百分比?
(4)若该学校有1500人,请你估计该学校选择乒乓球项目的学生人数约是多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() ,
,![]() ,
,![]() ;
;
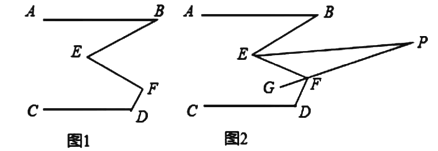
(1)若![]() ,则
,则![]() __________;
__________;
(2)请探索![]() 与
与![]() 之间满足的数量关系?说明理由;
之间满足的数量关系?说明理由;
(3)如图2,已知![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,反向延长
,反向延长![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com