
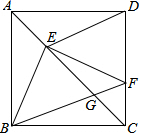
 如图,正方形ABCD的边长为1,点E、F分别在AC、DC上,若EC=BC,EF⊥BE,BF与EC交于点G,则$\frac{EG}{CG}$=$\sqrt{2}$.
如图,正方形ABCD的边长为1,点E、F分别在AC、DC上,若EC=BC,EF⊥BE,BF与EC交于点G,则$\frac{EG}{CG}$=$\sqrt{2}$. 分析 根据等腰三角形得出∠DEF=45°,再利用三角形全等得出EF=BE,进而得出△EGF~△BGC,利用相似三角形的性质得出BG•GF=EG•GC,进而得出GC=AE=$\sqrt{2}$,EG=1-GC=2-$\sqrt{2}$,即可得出结论.
解答 解:∵四边形ABCD是正方形,
∴∠BCA=∠DCA=45°,BC=DC=1,
∵EC=BC,
∴∠CBE=∠BEC=67.5°,
∵EF⊥BE,
∴∠CEF=22.5°,
∵EC=BC=DC,
∴∠DEF=45°,∠EDC=67.5°,
∴△EFD是等腰三角形,
∴ED=EF,
∵△BEC和△DEC是等腰三角形,且BC=CE=CD,
∴BE=ED,
∴BE=EF,
∴△BEF是等腰直角三角形,
∴∠GBC=∠EBC-∠EBF=67.5°-45°=22.5°=∠CEF,
∵∠EGF=∠BGC,
∴△EGF∽△BGC,
∴BG•GF=EG•GC,
∵CE=AB=CB=1,
∴AE=$\sqrt{2}$-1,
∴EG=EC-GC=2-$\sqrt{2}$,
∴$\frac{EG}{CG}$=$\frac{2-\sqrt{2}}{\sqrt{2}-1}$=$\sqrt{2}$,
故答案为:$\sqrt{2}$.
点评 此题考查了正方形的性质,相似三角形的判定和性质,等腰直角三角形的性质,等腰三角形的性质,熟练掌握相似三角形的判定和性质是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | a-4>b-4 | B. | -$\frac{a}{4}$<-$\frac{b}{4}$ | C. | 5a<5b | D. | ac<bc(c≠0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
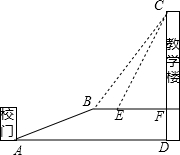 重庆市是著名的山城,重庆建筑多因地制宜,某中学依山而建,校门A处,有一斜坡AB,斜坡AB的坡度i=5:12,从A点沿斜坡行走了19.5米到达坡顶B处,在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=53°,离B点5米远的E处有一花台,在花台E处仰望C的仰角∠CEF=63.4°,CF的延长线交校门处的水平面于点D,则DC的长( )(参考数据:tan53°≈$\frac{4}{3}$,cos53°≈$\frac{3}{5}$,tan63.4°≈2,sin63.4°≈$\frac{9}{10}$)
重庆市是著名的山城,重庆建筑多因地制宜,某中学依山而建,校门A处,有一斜坡AB,斜坡AB的坡度i=5:12,从A点沿斜坡行走了19.5米到达坡顶B处,在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=53°,离B点5米远的E处有一花台,在花台E处仰望C的仰角∠CEF=63.4°,CF的延长线交校门处的水平面于点D,则DC的长( )(参考数据:tan53°≈$\frac{4}{3}$,cos53°≈$\frac{3}{5}$,tan63.4°≈2,sin63.4°≈$\frac{9}{10}$)| A. | 25 | B. | 27.5 | C. | 30 | D. | 32.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
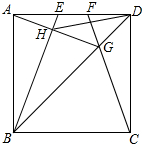 如图,在边长为4的正方形ABCD中,E、F是AD边上的两个动点,且AE=FD,连接BE、CF、BD,CF与BD交于点G,连接AG交BE于点H,连接DH,下列结论正确的个数是( )
如图,在边长为4的正方形ABCD中,E、F是AD边上的两个动点,且AE=FD,连接BE、CF、BD,CF与BD交于点G,连接AG交BE于点H,连接DH,下列结论正确的个数是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
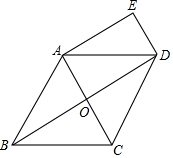 如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com