
分析 根据正多边形的中心角的求法公式分别求出中心角,根据正弦的定义求出边长,计算即可.
解答 解:正三角形的中心角是$\frac{360°}{3}$=120°,
则边长是:2×4sin60°=4$\sqrt{3}$,
正方形的中心角=$\frac{360°}{4}$=90°,
∴正方形的边长是:$\sqrt{{4}^{2}{+4}^{2}}$=4$\sqrt{2}$,
∴正三角形、正方形的边长之积是4$\sqrt{3}$×4$\sqrt{2}$=16$\sqrt{6}$,
故答案为:16$\sqrt{6}$.
点评 本题考查的是正多边形和圆,掌握正多边形的中心角的求法、掌握锐角三角函数的定义、熟记特殊角的三角函数值是解题的关键.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ABE=2∠C,AD是∠BAC的平分线,BE⊥AD,垂足为E
如图,在△ABC中,∠ABE=2∠C,AD是∠BAC的平分线,BE⊥AD,垂足为E查看答案和解析>>
科目:初中数学 来源: 题型:解答题
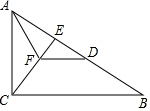 如图,在△ABC中,∠ACB=90°,CE是AB边上的高,AF平分∠CAB交CE于点F,过点F作FD∥CB交AB于点D.求证:AC=AD.
如图,在△ABC中,∠ACB=90°,CE是AB边上的高,AF平分∠CAB交CE于点F,过点F作FD∥CB交AB于点D.求证:AC=AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
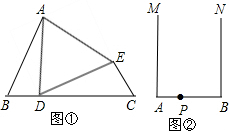
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 三边a、b、c | m | l×m | S |
| 3、4、5 | 2 | 24 | 6 |
| 5、12、13 | 4 | 120 | 30 |
| 8、15、17 | 6 | 240 | 60 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
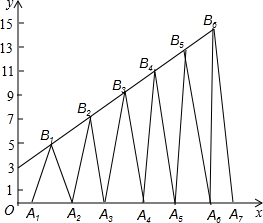 如图,已知B1(1,y1),B2(2,y2)B3(3,y3)…在直线y=2x+3上,在x轴上取点A1,使OA1=a(0<a<1);作等腰△A1B1A2面积为S1,等腰△A2B2A3面积为S2…;求S2017-S2016=4037-8072a.
如图,已知B1(1,y1),B2(2,y2)B3(3,y3)…在直线y=2x+3上,在x轴上取点A1,使OA1=a(0<a<1);作等腰△A1B1A2面积为S1,等腰△A2B2A3面积为S2…;求S2017-S2016=4037-8072a.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com