练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如果3a-5b =0，那么(a+b)︰b=        .
    8︰3；

    试题分析：3a-5b =0可得3a=5b。所以a=b，所以(a+b)︰b=（ b+b)
    点评：本题难度中等，主要考查学生对实数运算与代数式的掌握。为中考常考题型，要求学生牢固掌握解题技巧。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：不详 题型：单选题

    下列命题是真命题的是（   ）
    A．相等的角是对顶角
    B．三角形的一个外角大于任何一个内角
    C．一组邻边对应成比例的两个矩形相似
    D．若AB被点C黄金分割，则AC=AB

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    如图，在矩形ABCD中，对角线AC、BD相交于点G，E为AD的中点，连接BE交AC于点F，连接FD，若∠BFA＝90°，则下列四对三角形：①△BEA与△ACD；②△FED与△DEB；③△CFD与△ABC；④△ADF与△CFB．其中相似的为

    A．①④         B．①②             C．②③④           D．①②③

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

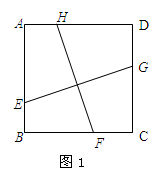
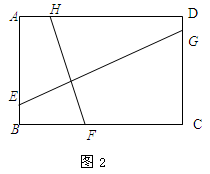
    （1）已知正方形ABCD ，点E、F、G、H分别在边AB、BC、CD、DA上，若EG⊥FH，求证EG = FH”（如图1）；

    （2）如果把条件中的“正方形”改为“长方形”，并设AB =2，BC =3（如图2），试探究EG、FH之间有怎样的数量关系，并证明你的结论；

    （3）如果把条件中的“EG⊥FH”改为“EG与FH的夹角为45°”，并假设正方形ABCD的边长为1，FH的长为（如图3），试求EG的长度。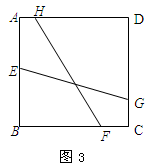

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    如图，点C在线段BD上，AB⊥BD，PD⊥BD，∠B=∠D=90°，AB=3，BC=6，CD=2，则当DE=         时，△ABC与△CDE相似．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    若△ABC∽△DEF，且面积比为1 ：9，则△ABC与△DEF的周长比为（ ）
    A．1 ：3B．1 ：9C．3 ：1D．1 ：81

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    小明和几位同学做手的影子游戏时，发现对于同一物体，影子的大小与光源到物体的距离有关.因此，他们认为：可以借助物体的影子长度计算光源到物体的位置.于是，他们做了以下尝试.
    （1）如图①，垂直于地面放置的正方形框架ABCD，边长AB为30cm，在其正上方有一灯泡，在灯泡的照射下，正方形框架的横向影子A′B，D′C的长度和为6cm.那么灯泡离地面的高度为           .
    （2）不改变①中灯泡的高度，将两个边长为30cm的正方形框架按图②摆放，请计算此时横向影子A′B，D′C的长度和为多少？
    （3）有n个边长为a的正方形按图③摆放，测得横向影子A′B，D′C的长度和为b,求灯泡离地面的距离.（写出解题过程，结果用含a,b,n的代数式表示）

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    △ADE∽△ABC， AM、AN分别是△ADE和△ABC的高，且周长分别是5和15，则AM：AN=      ．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    已知: == 且3a+2b-c="14" ,则 a+b+c 的值为            。

    查看答案和解析>>

    同步练习册答案