
分析 (1)超市为原点,以向东为正方向,根据货车从超市出发,向东走了1千米,到达小明家,继续向东走了3千米到达小兵家,然后西走了10千米,到达小华家,最后回到超市,即可表示出小明家、小兵家和小华家的具体位置;
(2)根据小华家距小明家是7个单位长度,即可得到距离;
(3)根据总路程以及货车行驶1千米的用油量为0.35升,即可得到货车从出发到结束行程共耗油的量.
解答 解:(1)小明家、小兵家和小华家的具体位置如下: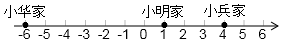
(2)根据数轴可知:小华家距小明家是7个单位长度,因而是7千米;
(3)由题意得,这辆货车一共行驶:1+3+10+6=20千米,
货车从出发到结束行程共耗油0.35×20=7升.
点评 本题考查了利用数轴表示一对具有相反意义的量,借助数轴,用几何方法解决问题,有直观、简捷,举重若轻的优势.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{1}{3}$ | C. | $\sqrt{2}$ | D. | 0.7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
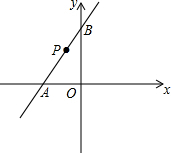 如图,在平面直角坐标系中,已知直线y=kx+6与x轴、y轴分别交于A、B两点,且△ABO的面积为12.
如图,在平面直角坐标系中,已知直线y=kx+6与x轴、y轴分别交于A、B两点,且△ABO的面积为12.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 数据 | 37 | 38 | 39 | 40 | 41 |
| 频数 | 8 | 4 | 5 | a | 1 |
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
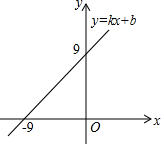 一次函数y=kx+b(k,b是常数,k≠0)的图象如图所示,则不等式kx+b>0的解集是( )
一次函数y=kx+b(k,b是常数,k≠0)的图象如图所示,则不等式kx+b>0的解集是( )| A. | x>-9 | B. | x>9 | C. | x<-9 | D. | x<9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0≤m≤1.5 | B. | m≥1.5 | C. | 0≤m≤1 | D. | 0<m≤1.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
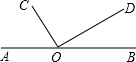 如图,O是直线AB上的一点,OC⊥OD,垂足为O.
如图,O是直线AB上的一点,OC⊥OD,垂足为O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com