
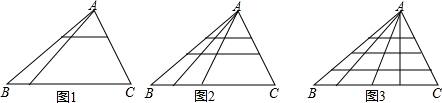
分析 设第n个图形三角形的个数为an(n为正整数),根据图形可得出根据分层来数出三角形的个数,写出部分an的值,根据数值的变化找出变化规律“an=$\frac{(n+1)^{2}(n+2)}{2}$”,依此规律即可解决问题.
解答 解:设第n个图形三角形的个数为an(n为正整数),
在图形中分层数三角形,
观察,发现规律:a1=2×(2+1)=6,a2=3×(3+2+1)=18,a3=4×(4+3+2+1)=40,…,
∴an=(n+1)•$\frac{(n+1)(n+2)}{2}$=$\frac{(n+1)^{2}(n+2)}{2}$.
当n=8时,a8=$\frac{{9}^{2}×10}{2}$=405(个).
故答案为:405.
点评 本题考查了规律型中得图形的变化类,解题的关键是找出变化规律“an=$\frac{(n+1)^{2}(n+2)}{2}$”.本题属于基础题,难度不大,解决该题型题目时,根据给定的图形找出部分an的值,再根据数的变化找出变化规律是关键.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:填空题
 如图,在?ABCD中,∠1=∠2,∠3=∠4,EF∥AD,请直接写出与AE相等的线段DF=FE,DF=AE(两条即可),写出满足勾股定理的等式CG2+DG2=CD2(一组即可)
如图,在?ABCD中,∠1=∠2,∠3=∠4,EF∥AD,请直接写出与AE相等的线段DF=FE,DF=AE(两条即可),写出满足勾股定理的等式CG2+DG2=CD2(一组即可)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
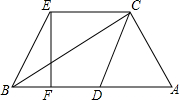 如图,在Rt△ABC中,∠ACB=90°,点D是AB上的一点,连接CD,CE∥AB,BE∥CD,且CE=AD.
如图,在Rt△ABC中,∠ACB=90°,点D是AB上的一点,连接CD,CE∥AB,BE∥CD,且CE=AD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com