
分析 (1)原式利用算术平方根,立方根的定义,以及二次根式性质化简即可得到结果;
(2)原式各项化简后,合并即可得到结果;
(3)原式利用二次根式乘除法则计算即可得到结果;
(4)原式利用完全平方公式展开,计算即可得到结果.
解答 解:(1)原式=4-3+3$\sqrt{3}$-3=3$\sqrt{3}$-2;
(2)原式=3$\sqrt{2}$+$\sqrt{2}$-2$\sqrt{2}$=2$\sqrt{2}$;
(3)原式=$\sqrt{27÷3}$+$\sqrt{3÷3}$-$\sqrt{18÷2}$=3+1-3=1;
(4)原式=12-4$\sqrt{3}$+1=13-4$\sqrt{3}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:解答题
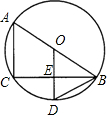 如图,AB是⊙O的直径,CB是弦,OD⊥CB于E,交$\widehat{CB}$于D,连接AC.
如图,AB是⊙O的直径,CB是弦,OD⊥CB于E,交$\widehat{CB}$于D,连接AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com