
已知:二次函数 (m为常数).
(m为常数).
(1)若这个二次函数的图象与x轴只有一个公共点A,且A点在x轴的正半轴上.
①求m的值;
②四边形AOBC是正方形,且点B在y轴的负半轴上,现将这个二次函数的图象平移,使平移后的函数图象恰好经过B,C两点,求平移后的图象对应的函数解析式;
(2) 当0≤ ≤2时,求函数
≤2时,求函数 的最小值(用含m的代数式表示).
的最小值(用含m的代数式表示).

解:(1)①∵ 二次函数 的图象与x轴只有一个公共点A,
的图象与x轴只有一个公共点A,
∴ 
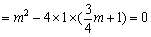 .
.
整理,得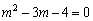 .
.
解得,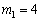 ,
,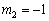 .
.
又点A在x轴的正半轴上,
∴ 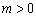 .
.
∴ m=4.
②由①得点A的坐标为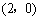 .
.
∵ 四边形AOBC是正方形,点B在y轴的负半轴上,
∴ 点B的坐标为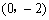 ,点C的坐标为
,点C的坐标为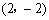 .
.
设平移后的图象对应的函数解析式为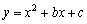 (b,c为常数).
(b,c为常数).
∴ 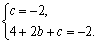
解得
∴平移后的图象对应的函数解析式为 .
.
(2)函数 的图象是顶点为
的图象是顶点为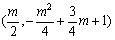 ,且开口向上的抛物线.分三种情况:
,且开口向上的抛物线.分三种情况:
(ⅰ)当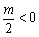 ,即
,即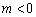 时,函数在0≤
时,函数在0≤ ≤2内y随x的增大而增大,此时函数的最小值为
≤2内y随x的增大而增大,此时函数的最小值为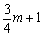 ;
;
(ⅱ)当0≤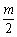 ≤2,即0≤
≤2,即0≤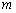 ≤4时,函数的最小值为
≤4时,函数的最小值为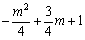 ;
;
(ⅲ)当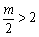 ,即
,即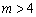 时,函数在0≤
时,函数在0≤ ≤2内y随x的增大而减小,此时函数的最小值为
≤2内y随x的增大而减小,此时函数的最小值为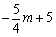 .
.
综上,当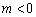 时,函数
时,函数 的最小值为
的最小值为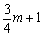 ;
;
当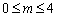 时,函数
时,函数 的最小值为
的最小值为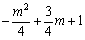 ;
;
当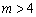 时,函数
时,函数 的最小值为
的最小值为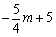 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
如图,在△ABC中,∠ACB=90°,∠ABC=30°,BC=2.将△ABC绕点C逆时针旋转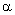 角后得到△A′B′C,当点A的对应点A' 落在AB边上时,旋转角
角后得到△A′B′C,当点A的对应点A' 落在AB边上时,旋转角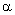 的度数是 度,阴影部分的面积为 .
的度数是 度,阴影部分的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB是⊙O的弦,OC⊥AB于点C,连接OA,AB=12, .
.
(1)求OC的长;
(2)点E,F在⊙O上,EF∥AB.若EF=16,直接写出EF与AB之间的距离.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
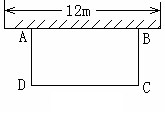
如图,科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD,
其中一边AB靠墙,墙长为12m,设AD的长为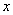 m,DC的长为
m,DC的长为 m.
m.
(1)求 与
与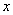 之间的函数关系式;
之间的函数关系式;
(2)若围成矩形科技园ABCD的三边材料总长不超过26m,材料AD和
DC的长都是整米数,求出满足条件的所有围建方案.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com