
【题目】如图,矩形ABCD的面积为1cm2,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B…;依此类推,则平行四边形AO2016C2017B的面积为_____.

【答案】![]()
【解析】
矩形ABCD的面积=AB×AD=1,过点O向AB作垂线,垂足为E,平行四边形AOC1B的面积=AB×OE,根据矩形的性质,OE=![]() AD,即平行四边形AOC1B的面积=AB×
AD,即平行四边形AOC1B的面积=AB×![]() AD=
AD=![]() ,过点O1向AB作垂线,垂足为F,根据平行四边形的性质,O1F=
,过点O1向AB作垂线,垂足为F,根据平行四边形的性质,O1F=![]() OE=
OE=![]() AD,即平行四边形AO1C2B面积=AB×
AD,即平行四边形AO1C2B面积=AB×![]() AD=
AD=![]() ,依此类推,即可得到平行四边形AO2016C2017B的面积.
,依此类推,即可得到平行四边形AO2016C2017B的面积.
解:过点O向AB作垂线,垂足为E,过点O1向AB作垂线,垂足为F,如下图所示:
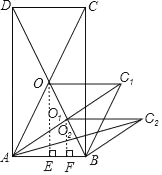
∵∠DAB=∠OEB,
∴OE∥DA,
∵O为矩形ABCD的对角线交点,
∴OB=OD
∴OE=![]() AD,
AD,
矩形ABCD的面积=AB×AD=1,
平行四边形AOC1B的面积=AB×OE=AB×![]() AD=
AD=![]() ,
,
同理,根据平行四边形的性质,
O1F=![]() OE=
OE=![]() AD,
AD,
平行四边形AO1C2B面积=AB×![]() AD=
AD=![]() ,
,
依此类推:
平行四边形AO2016C2017B的面积=AB×![]() AD=
AD=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,![]() ,
,![]() ,
,![]() ,点E为CD上一动点,经过A、C、E三点的
,点E为CD上一动点,经过A、C、E三点的![]() 交BC于点F.
交BC于点F.
(操作与发现)
![]() 当E运动到
当E运动到![]() 处,利用直尺与规作出点E与点F;
处,利用直尺与规作出点E与点F;![]() 保留作图痕迹
保留作图痕迹![]()
![]() 在
在![]() 的条件下,证明:
的条件下,证明:![]() .
.
(探索与证明)
![]() 点E运动到任何一个位置时,求证:
点E运动到任何一个位置时,求证:![]() ;
;
(延伸与应用)
![]() 点E在运动的过程中求EF的最小值.
点E在运动的过程中求EF的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
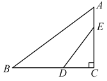
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,tanA=![]() .点D,E分别是边BC,AC上的点,且∠EDC=∠A.将△ABC沿DE所在直线对折,若点C恰好落在边AB上,则DE的长为___.
.点D,E分别是边BC,AC上的点,且∠EDC=∠A.将△ABC沿DE所在直线对折,若点C恰好落在边AB上,则DE的长为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有三个点A(2,3),B(1,1),C(4,2)
(1)连接A、B、C三点,请在如图中作出△ABC关于x轴对称的图形△A’B’C’并直接写出各对称点的坐标;(2)求△ABC的面积;(3)若M(x,y)是△ABC内部任意一点,请直接写出点M在△A’B’C’内部的对应点M1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABD与等边△ACE,连接BE、CD,BE的延长线与CD交于点F,下列结论:(1)BE=CD ;(2)AF平分∠EAC ; (3)∠BFD=60°;(4)AF+FD=BF 其中正确的有( )
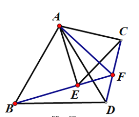
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年我市体育中考总分60分,其中男生1000米跑为必选项目,再在立定跳远、跳绳、实心球掷远、篮球运球和足球运球中选择两项;女生800米跑为必选项目,再在立定跳远、跳绳、仰卧起坐、篮球运球和足球运球中选择两项![]() 某校对得分超过40分的20位学生的成绩m进行统计,结果如频数分布表所示:
某校对得分超过40分的20位学生的成绩m进行统计,结果如频数分布表所示:

![]() 求a的值;
求a的值;
![]() 若用扇形图来描述,求分数在
若用扇形图来描述,求分数在![]() 内所对应的扇形图的圆心角的大小;
内所对应的扇形图的圆心角的大小;
![]() 若男生小明在刚开始训练时在选考项目随机选择两项进行训练,试用列举法求小明选择”跳绳
若男生小明在刚开始训练时在选考项目随机选择两项进行训练,试用列举法求小明选择”跳绳![]() 篮球运球“的概率
篮球运球“的概率![]() 提示:可以用字母表示各个项目
提示:可以用字母表示各个项目![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市创建“绿色发展模范城市”,针对境内长江段两种主要污染源:生活污水和沿江工厂污染物排放,分别用“生活污水集中处理”(下称甲方案)和“沿江工厂转型升级”(下称乙方案)进行治理,若江水污染指数记为Q,沿江工厂用乙方案进行一次性治理(当年完工),从当年开始,所治理的每家工厂一年降低的Q值都以平均值n计算.第一年有40家工厂用乙方案治理,共使Q值降低了12.经过三年治理,境内长江水质明显改善.
(1)求n的值;
(2)从第二年起,每年用乙方案新治理的工厂数量比上一年都增加相同的百分数m,三年来用乙方案治理的工厂数量共190家,求m的值,并计算第二年用乙方案新治理的工厂数量;
(3)该市生活污水用甲方案治理,从第二年起,每年因此降低的Q值比上一年都增加个相同的数值a.在(2)的情况下,第二年,用乙方案所治理的工厂合计降低的Q值与当年因甲方案治理降低的Q值相等,第三年,用甲方案使Q值降低了39.5.求第一年用甲方案治理降低的Q值及a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.

下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.
其中合理的是( )
A. ① B. ② C. ①② D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB,CD都是![]() 的直径,连接DB,过点C的切线交DB的延长线于点E.
的直径,连接DB,过点C的切线交DB的延长线于点E.
![]() 如图1,求证:
如图1,求证:![]() ;
;
![]() 如图2,过点A作
如图2,过点A作![]() 交EC的延长线于点F,过点D作
交EC的延长线于点F,过点D作![]() ,垂足为点G,求证:
,垂足为点G,求证:![]() ;
;
![]() 如图3,在
如图3,在![]() 的条件下,当
的条件下,当![]() 时,在
时,在![]() 外取一点H,连接CH、DH分别交
外取一点H,连接CH、DH分别交![]() 于点M、N,且
于点M、N,且![]() ,点P在HD的延长线上,连接PO并延长交CM于点Q,若
,点P在HD的延长线上,连接PO并延长交CM于点Q,若![]() ,
,![]() ,
,![]() ,求线段HM的长.
,求线段HM的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com