
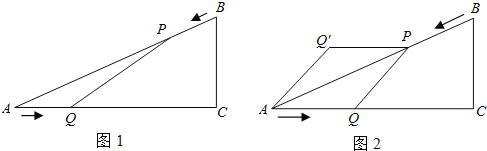
【题目】如图1,已知△ABC中,AB=10cm,AC=8cm,BC=6 cm ,如果点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm /s,连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
(1)当t为何值时,PQ∥BC.
(2)是否存在某时刻t,使线段PQ恰好把△ABC的面积平分?若存在求出此时t的值;若不存在,请说明理由.
(3)如图2,把△APQ沿AP翻折,得到四边形AQPQ′.那么是否存在某时刻t使四边形AQPQ′为菱形?若存在,求出此时菱形的面积;若不存在,请说明理由.
【答案】(1)当![]() s时,PQ∥BC.(2)不存在某时刻t,使线段PQ恰好把△ABC的面积平分.(3)存在时刻t,使四边形AQPQ′为菱形,此时菱形的面积为
s时,PQ∥BC.(2)不存在某时刻t,使线段PQ恰好把△ABC的面积平分.(3)存在时刻t,使四边形AQPQ′为菱形,此时菱形的面积为![]() cm2.
cm2.
【解析】(1)证△APQ∽△ABC,推出![]() =
=![]() ,代入得出
,代入得出![]() =
=![]() ,求出方程的解即可;(2)假设存在某时刻t,使线段PQ恰好把△ABC的面积平分,得出方程-
,求出方程的解即可;(2)假设存在某时刻t,使线段PQ恰好把△ABC的面积平分,得出方程-![]() t2+6t=
t2+6t=![]() ×
×![]() ×8×6,求出此方程无解,即可得出答案.
×8×6,求出此方程无解,即可得出答案.
(3)首先根据菱形的性质及相似三角形比例线段关系,求得PQ、OD、和PD的长度;然后在Rt△PQD中,根据勾股定理列出方程(8-![]() t)2-(6-
t)2-(6-![]() t)2=(2t)2,求得时间t的值;最后根据菱形的面积等于△AQP的面积的2倍,进行计算即可.
t)2=(2t)2,求得时间t的值;最后根据菱形的面积等于△AQP的面积的2倍,进行计算即可.
解:(1)BP=2t,则AP=10﹣2t.
∵PQ∥BC,
∴△APQ∽△ABC,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,
,
解得:t=![]() ,
,
∴当t=![]() 时,PQ∥BC.
时,PQ∥BC.
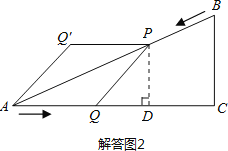
(2)如答图1所示,过P点作PD⊥AC于点D.

∴PD∥BC,∴![]() ,即
,即![]() ,解得
,解得![]() .
.
![]() ,
,
假设存在某时刻t,使线段PQ恰好把△ABC的面积平分,
则有S△AQP= ![]() S△ABC,而S△ABC=
S△ABC,而S△ABC=![]() ACBC=24,∴此时S△AQP=12.
ACBC=24,∴此时S△AQP=12.
S△AQP![]() ,
,
∴![]() ,化简得:t2﹣5t+10=0,
,化简得:t2﹣5t+10=0,
∵△=(﹣5)2﹣4×1×10=﹣15<0,此方程无解,
∴不存在某时刻t,使线段PQ恰好把△ABC的面积平分.
(3)假设存在时刻t,使四边形AQPQ′为菱形,则有AQ=PQ=BP=2t.
如答图2所示,过P点作PD⊥AC于点D,则有PD∥BC,
∴![]() ,即
,即![]() ,
,
解得: ![]() ,
, ![]() ,
,
∴QD=AD﹣AQ= ![]() .
.
在Rt△PQD中,由勾股定理得:QD2+PD2=PQ2,
即![]() ,
,
化简得:13t2﹣90t+125=0,
解得:t1=5,t2= ![]() ,
,
∵t=5s时,AQ=10cm>AC,不符合题意,舍去,∴t=![]() .
.
由(2)可知,S△AQP=![]()
∴S菱形AQPQ′=2S△AQP=2×![]() =
=![]() cm2.
cm2.
所以存在时刻t,使四边形AQPQ′为菱形,此时菱形的面积为![]() cm2.
cm2.
“点睛”本题考查了三角形的面积,勾股定理的逆定理,相似三角形的性质和判定的应用,主要考查学生综合运用进行推理和计算的能力.解决问题的关键是作辅助线构造相似三角形以及直角三角形,根据相似三角形的对应边成比例以及勾股定理进行列式求解.


科目:初中数学 来源: 题型:
【题目】△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件20元,售价为每件30元,每个月可卖出180件;如果每件商品的售价每上涨1元,则每个月就会少卖出10件,但每件售价不能高于35元,设每件商品的售价上涨x元(x为整数),每个月的销售利润为y元.
(1)求y与x的函数关系式,并直接写出自变量x的取值范围;求x为何值时y的值为1920?
(2)每件商品的售价为多少元时,每个月可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子,或可以求出一些不规则图形的面积. 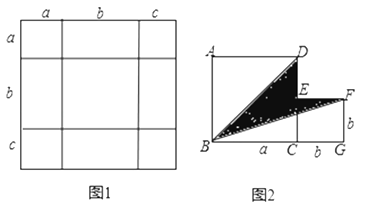
(1)如图1,是将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的方法计算这个图形的面积,你能发现什么结论,请写出来.
(2)如图2,是将两个边长分别为a和b的正方形拼在一起,B、C、G三点在同一直线上,连接BD和BF,若两正方形的边长满足a+b=10,ab=20,你能求出阴影部分的面积吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=45°,点P在∠AOB内部,P1与P关于OB对称,P2与P关于OA对称,则P1 , O,P2三点构成的三角形是( )
A.直角三角形
B.等腰三角形
C.等边三角形
D.等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
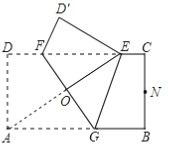
【题目】如图,矩形纸片ABCD中,AD=1,AB=2.将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB、CD交于点G、F,AE与FG交于点O.当△AED的外接圆与BC相切于BC的中点N.则折痕FG的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E为等腰△ABC的底边BC上一动点,过E作EF⊥BC交AB于D,交CA的延长线于F,问: 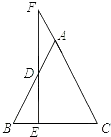
(1)∠F与∠ADF的关系怎样?说明理由;
(2)若E在BC延长线上,其余条件不变,上题的结论是否成立?若不成立,说明理由;若成立,画出图形并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,CD⊥AB于点D,BE⊥AC于点E,BE与CD相交于点O. 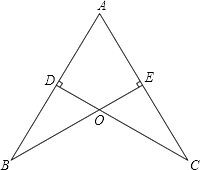
(1)求证:AD=AE;
(2)试猜想:OA与BC的位置关系,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com