练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    问题解决：
    精英家教网
    分析：根据题中的等量关系可以列出方程组解方程组即可．
    解答：解：设一盒饼干需x元钱，一袋牛奶需y元钱，由题意得：
    x-y=7
    0.8x+y＜10
    ，且x+y＞10，
    解得8.5＜x＜9.4，1.5＜y＜2.4．
    答：一盒饼干需大于8.5元且小于9.4元钱，一袋牛奶需大于1.5元且小于2.4元钱．
    点评：解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程组，再求解．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：阅读理解

    探究题：
    数学问题：各边长都是整数，最大边长为21的三角形有多少个？
    为解决上面的数学问题，我们先研究下面的数学模型：
    数学模型：在1～21这21个自然数中，每次取两个不同的数，使得所取的两个数之和大于21，有多少种不同取法？
    为找到解决问题的方法，我们把上面数学模型简单化．
    （1）在1～4这4个自然数中，每次取两个不同的数，使得所取的两个数之和大于4，有多少种取法？
    根据题意，有下列取法：1+4，2+3，2+4，3+2，3+4，4+1，4+2，4+3，而1+4与4+1，2+3与3+2，…是同一种取法，所以上述每一种取法都重复过一次，因此共有
    1+2+2+3
    2
    =4=
    42
    4
    种不同的取法．
    （2）在1～5这5个自然数中，每次取两个不同的数，使得所取的两个数之和大于5，有多少种取法？
    根据题意，有下列取法：1+5，2+4，2+5，3+4，3+5，4+2，4+3，4+5，5+1，5+2，5+3，5+4，而1+5与5+1，2+4与4+2，…是同一种取法，所以上述每一种取法都重复过一次，因此共有
    1+2+2+3+4
    2
    =6=
    52-1
    4
    种不同的取法．
    （3）在1～6这6个自然数中，每次取两个不同的数，使得所取的两个数之和大于6，有多少种不同的取法？
    根据题意，有下列取法：1+6，2+5，2+6，3+4，3+5，3+6，4+3，4+5，4+6，5+2，5+3，5+4，5+6，6+1，6+2，6+3，6+4，6+5，而1+6与6+1，2+5与5+2，…是同一种取法，所以上述每一种取法都重复过一次，因此共有
    1+2+3+3+4+5
    2
    =9=
    62
    4
    种不同的取法．
    （4）在1～7这7个自然数中，每次取两个不同的数，使得所取的两个数之和大于7，有多少种取法？
    根据题意，有下列取法：1+7，2+6，2+7，3+5，3+6，3+7，4+5，4+6，4+7，5+3，5+4，5+6，5+7，6+2，6+3，6+4，6+5，6+7，7+1，7+2，7+3，7+4，7+5，7+6，而1+7与7+1，2+6与6+2，…是同一种取法，所以上述每一种取法都重复过一次，因此共有
    1+2+3+3+4+5+6
    2
    =12=
    72-1
    4
    种不同的取法…
    问题解决
    仿照上述研究问题的方法，解决上述数学模型和提出的问题
    （1）在1～21这21个自然数中，每次取两个不同的数，使得所取的两个数之和大于21，共有
     
    种不同取法；（只填结果）
    （2）在1～n（n为偶数）这n个自然数中，每次取两个数，使得所取的两个数字之和大于n，共有
     
    种不同取法；（只填最简算式）
    （3）在1～n（n为奇数）这n个自然数中，每次取两个数，使得所取的两个数之和大于n，共有
     
    种不同取法；（只填最简算式）
    （4）各边长都是整数且不相等，最大边长为21的三角形有多少个？（写出最简算式和结果，不写分析过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    23、动手操作：
    如图①是一个长为2a，宽为2b的长方形，沿图中的虚线剪开分成四个大小相等的长方形，然后按照图②所示拼成一个正方形．
    提出问题：
    （1）观察图②，请用两种不同的方法表示阴影部分的面积；
    （2）请写出三个代数式（a+b）2，（a-b）2，ab之间的一个等量关系．
    问题解决：
    根据上述（2）中得到的等量关系，解决下列问题：
    已知：x+y=6，xy=3．求：（x-y）2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

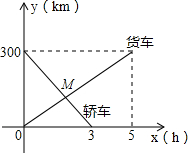    （2013•太原二模）已知一辆货车从A地开往B地，一辆轿车从B地开往A地，两车同时出发，设货车离A地的距离为y1（km），轿车离A地的距离为y2（km），行驶时间为x（h）．y1，y2与x的函数关系图象如图．
    解读信息：
    （1）A，B两地之间的距离为
    300
    300
    km；
    （2）y1与x的函数关系式为
    y1=60x（0≤x≤5）
    y1=60x（0≤x≤5）
    ，y2与x的函数关系式为
    y2=-100x+300（0≤x≤3）
    y2=-100x+300（0≤x≤3）
    ；
    问题解决：
    （3）设货车、轿车之间的距离为s（km），求s与货车行驶时间x（h）的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    问题探究
    （1）如图1，△ABC是钝角三角形，∠C＞90°请在图1中，将△ABC补成矩形，使△ABC的两个顶点为矩形一边的两个端点，第三个顶点落在矩形这一边的对边上．
    （2）如图2，△ABC是直角三角形，∠C=90°，AC=12，BC=5．请在图2中，将△ABC补成矩形，使得△ABC的两个顶点为矩形一边的两个端点，第三个顶点落在矩形这一边的对边上，画出所有符合条件的矩形，并求此矩形的面积．
    问题解决
    （3）李大爷现有一个锐角三角形ABC（AB＞AC＞BC）形的鱼塘（如图3），鱼塘三个角的顶点A、B、C上各有一棵大树．现在李大爷想把原来的鱼塘扩建成一个矩形鱼塘（原鱼塘周围的面积足够大），并还想：三棵大树A、B、C中的两个为矩形鱼塘一边的两个端点，第三棵树落在鱼塘这一边的对边上．请你在图3中，画出所有符合条件的矩形鱼塘的示意图，并指出哪一个的周长最小？说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    实际背景预警方案确定：
    设W=
    当月的500克猪肉价格
    当月的500克玉米价格
    ．如果当月W＜6，则下个月要采取措施防止“猪贱伤农”．
    数据收集：
    今年2月～5月玉米、猪肉价格统计表
    月份 2 3 4 5
    玉米价格（元/500克） 0.7 0.8 0.9 1
    猪肉价格（元/500克） 7.5 m 6.25 6
    问题解决：
    （1）若今年3月的猪肉价格比上月下降的百分数与5月的猪肉价格比上月下降的百分数相等，求3月的猪肉价格m；
    （2）若今年6月及以后月份，玉米价格增长的规律不变，而每月的猪肉价格按照5月的猪肉价格比上月下降的百分数继续下降，请你预测7月时是否要采取措施防止“猪贱伤农”？

    查看答案和解析>>

    同步练习册答案