
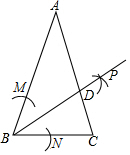
 △ABC中,AB=AC,∠ABC=72°,以B为圆心,以任意长为半径画弧,分别交BA、BC于M、N,再分别以M、N为圆心,以大于$\frac{1}{2}$MN为半径画弧,两弧交于点P,射线BP交AC于点D,则图中与BC相等的线段有( )
△ABC中,AB=AC,∠ABC=72°,以B为圆心,以任意长为半径画弧,分别交BA、BC于M、N,再分别以M、N为圆心,以大于$\frac{1}{2}$MN为半径画弧,两弧交于点P,射线BP交AC于点D,则图中与BC相等的线段有( )| A. | BD | B. | CD | C. | BD和AD | D. | CD和AD |
分析 由基本作图得到BP平分∠ABC,所以∠ABP=∠CBP=36°,则利用等腰三角形的性质得∠C=∠ABC=72°,再利用三角形内角和定理计算出∠A=36°,于是得到AD=BD,然后计算出∠BDC=72°,从而得到∠BDC=∠C,所以BD=BC.
解答 解:由画法得BP平分∠ABC,则∠ABP=∠CBP=$\frac{1}{2}∠$ABC=$\frac{1}{2}$×72°=36°,
∵AB=AC,
∴∠C=∠ABC=72°,
∴∠A=180°-2×72°=36°,
∴∠A=∠ABD,
∴AD=BD,
∵∠BDC=∠A+∠ABD=72°,
∴∠BDC=∠C,
∴BD=BC,
即BC=BD=AD.
故选C.
点评 本题考查了作图-基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了等腰三角形的判定与性质.


科目:初中数学 来源: 题型:选择题
| A. | 两个锐角对应相等 | B. | 一个锐角、一条直角边对应相等 | ||
| C. | 两条直角边对应相等 | D. | 一条斜边、一条直角边对应相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1-10%+15%)x万元 | B. | (1+10%-15%)x万元 | C. | (1-10%)(1+15%)x万元 | D. | (x-10%)(x+15%)万元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | c2-a2=b2 | B. | ∠A-∠C=∠B | C. | a:b:c=20:21:29 | D. | ∠A:∠B:∠C=2:3:4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 为减少雾霾天气,我们崇尚低碳生活,现有一个正方体的每个面都写有一个汉字,其平面展开图如图所示,则在该正方体中,和”崇“相对的面上写的汉字是( )
为减少雾霾天气,我们崇尚低碳生活,现有一个正方体的每个面都写有一个汉字,其平面展开图如图所示,则在该正方体中,和”崇“相对的面上写的汉字是( )| A. | 低 | B. | 碳 | C. | 生 | D. | 活 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6cm | B. | 7cm | C. | 8cm | D. | 10cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com