
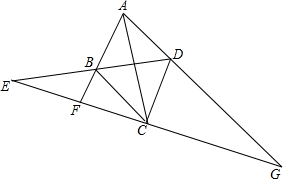
 已知:如图,菱形ABCD,分别延长AB、DB、AD交直线EC于E、F、G,且AG=2AF,求证:EB=BD.
已知:如图,菱形ABCD,分别延长AB、DB、AD交直线EC于E、F、G,且AG=2AF,求证:EB=BD. 分析 由菱形的性质得出BC=CD,AB∥CD,AD∥BC,证出△AFG∽△DCG,得出对应边成比例$\frac{AG}{AF}=\frac{DG}{DC}$,由已知得出DG=2DC=2BC,由平行线证出△CBE∽△GDE,得出$\frac{BE}{DE}=\frac{BC}{DG}$=$\frac{1}{2}$,即可得出结论.
解答 证明:∵四边形ABCD是菱形,
∴BC=CD,AB∥CD,AD∥BC,
∴△AFG∽△DCG,
∴$\frac{AG}{AF}=\frac{DG}{DC}$,
∵AG=2AF,
∴DG=2DC=2BC,
∵AG∥BC,
∴△CBE∽△GDE,
∴$\frac{BE}{DE}=\frac{BC}{DG}$=$\frac{1}{2}$,
∴EB=BD.
点评 本题考查了菱形的性质、相似三角形的判定与性质;熟练掌握菱形的性质,证明三角形相似是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
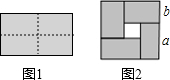 如图1是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空的部分的面积( )
如图1是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空的部分的面积( )| A. | a2-b2 | B. | 2ab | C. | (a+b)2 | D. | (a-b)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知顶点为A(2,-1)的抛物线经过点B(0,3),与x轴交于C、D两点(点C在点D的左侧);
已知顶点为A(2,-1)的抛物线经过点B(0,3),与x轴交于C、D两点(点C在点D的左侧);查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 现有某教学网站策划了A、B两种上网学习的月收费方式:
现有某教学网站策划了A、B两种上网学习的月收费方式:| 收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
| A | 7 | 25 | 0.01 |
| B | m | n | 0.01 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ① | B. | ③ | C. | ②③ | D. | ③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com