
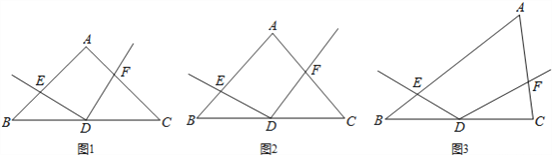
【题目】如图,在△ABC中,点D为BC边的中点,以D为顶点的∠EDF的两边分别与AB、AC交于点E、F,且∠EDF与∠A互补.
(1)如图①,若AB=AC,且∠A=90°,证明:DE=DF;
(2)如图②,若AB=AC,那么(1)中的结论是否成立?请说明理由.
(3)如图③,若![]() ,探索线段DE与DF的数量关系,并证明你的结论.
,探索线段DE与DF的数量关系,并证明你的结论.
【答案】(1)见解析;(2)成立,理由见解析;(3)![]() ,理由见解析
,理由见解析
【解析】分析:(1)首先根据等腰三角形的性质可得∠DAB=∠DAC=![]() ∠BAC,AD⊥BC,再证明∠C=∠B=45°,∠ADE=∠FDC,AD=DC可以利用ASA定理证明△AED≌△CFD,进而得到DE=DF;
∠BAC,AD⊥BC,再证明∠C=∠B=45°,∠ADE=∠FDC,AD=DC可以利用ASA定理证明△AED≌△CFD,进而得到DE=DF;
(2)DE=DF依然成立.如图2,过点D作DM⊥AB于M,作DN⊥AC于N,连接AD,则∠EMD=∠FND=90°,由于AB=AC,点D为BC中点,根据三角形的性质三线合一得到AD平分∠BAC,于是得到DM=DN,在四边形AMDN中.,∠DMA=∠DNA=90°,得到∠MAN+∠MDN=180°,又由于∠EDF与∠MAN互补,证得∠MDN=∠EDF,推出△DEM≌△DFN(ASA),即可得到结论;
(3)结论DE:DF=n:m.如图3,过点D作DM⊥AB于M,作DN⊥AC于N,连接AD同(2)可证∠1=∠2,通过△DEM∽△DFN,得到![]() .由于点E为AC的中点,得到S△ABD=S△ADC,列等积式即可得到结论.
.由于点E为AC的中点,得到S△ABD=S△ADC,列等积式即可得到结论.
详解:(1)DF=DE,
理由:如图1,连接AD,
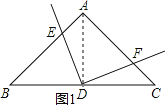
∵Rt△ABC是等腰三角形,
∴∠C=∠B=45°,
∴D是斜边BC的中点,
∴∠DAB=∠DAC=![]() ∠BAC=45°,AD⊥BC,
∠BAC=45°,AD⊥BC,
∴AD=DC,
∵∠EDF=90°,
∴∠ADF+∠ADE=90°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠ADF+∠FDC=90°,
∴∠ADE=∠FDC,
在△ADE和△CDF中,
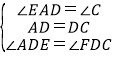 ,
,
∴△AED≌△CFD(ASA);
∴DE=DF;
(2)DE=DF依然成立.
如图2,过点D作DM⊥AB于M,作DN⊥AC于N,连接AD,
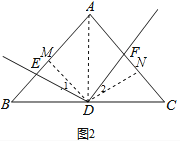
则∠EMD=∠FND=90°,
∵AB=AC,点D为BC中点,
∴AD平分∠BAC,
∴DM=DN,
∵在四边形AMDN中.,∠DMA=∠DNA=90°,
∴∠MAN+∠MDN=180°,
又∵∠EDF与∠MAN互补,
∴∠MDN=∠EDF,
∴∠1=∠2,
在△DEM与△DFN中,
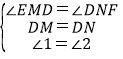 ,
,
∴△DEM≌△DFN(ASA),
∴DE=DF.
(3)结论DE:DF=n:m.
如图3,过点D作DM⊥AB于M,作DN⊥AC于N,连接AD,

同(2)可证∠1=∠2,
又∵∠EMD=∠FND=90°,
∴△DEM∽△DFN,
∴![]() .
.
∵点D为BC边的中点,
∴S△ABD=S△ADC,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
【题目】发现问题、探索规律,要有一双敏锐的双眼,下面的图形是由边长为1的小正方形按照某种规律排列而成的.

(1)观察图形,填写下表:
图形个数(n) | (1) | (2) | (3) |
正方形的个数 | 8 |
|
|
图形的周长 | 18 |
|
|
(2)推测第n个图形中,正方形有 个,周长为 .
(3)写出第30个图形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD在平面直角坐标系的第一象限内,BC与x轴平行,AB=1,点C的坐标为(6,2),E是AD的中点;反比例函数y1=![]() (x>0)图象经过点C和点E,过点B的直线y2=ax+b与反比例函数图象交于点F,点F的纵坐标为4.
(x>0)图象经过点C和点E,过点B的直线y2=ax+b与反比例函数图象交于点F,点F的纵坐标为4.
(1)求反比例函数的解析式和点E的坐标;
(2)求直线BF的解析式;
(3)直接写出y1>y2时,自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中:
①0是最小的整数;
②有理数不是正数就是负数;
③正整数、负整数、正分数、负分数统称为有理数;
④非负数就是正数;
⑤![]() 不仅是有理数,而且是分数;
不仅是有理数,而且是分数;
⑥![]() 是无限不循环小数,所以不是有理数;
是无限不循环小数,所以不是有理数;
⑦无限小数不都是有理数;
⑧正数中没有最小的数,负数中没有最大的数.
其中错误的说法的个数为( )
A.7个B.6个C.5个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学老师布置了一道思考题“计算:(-![]() )÷(
)÷(![]()
![]() )”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.
)”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.
小明的解法:原式的倒数为(![]()
![]() )÷(
)÷(![]() )=(
)=(![]()
![]() )×(-12)=-4+10=6,所以(-
)×(-12)=-4+10=6,所以(-![]() )÷(
)÷(![]()
![]() )=
)=![]() .
.
(1)请你判断小明的解答是否正确,并说明理由.
(2)请你运用小明的解法解答下面的问题.
计算:(-![]() )÷(
)÷(![]()
![]() +
+![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.
MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线a、b分别与∠A的两边相交,且a∥b.下列各角的度数关系正确的是( )
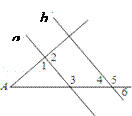
A. ∠2+∠5>180° B. ∠2+∠3<180° C. ∠1+∠6>180° D. ∠3+∠4<180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=10,P是线段AB上的动点,分别以AP、PB为边在线段AB的同侧作等边△ACP和△PDB,连接CD,设CD的中点为G,当点P从点A运动到点B时,则点G移动路径的长是_________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片ABCD的∠C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部的点E处,若FH平分∠BFE,则∠GFH的度数是( )

A.110°B.100°C.90°D.80°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com