Question

10．（1）如图所示，∠AOB=α，∠AOB内有一点P，在∠AOB的两边上有两个动点Q、R（均不同于点O），现在把△PQR周长最小时∠QPR的度数记为β，则α与β应该满足关系是β+2α=180°．
（2）设一次函数y=mx-3m+4（m≠0）对于任意两个m的值m₁、m₂分别对应两个一次函数y₁、y₂，若m₁m₂＜0，当x=a时，取相应y₁、y₂中的较小值P，则P的最大值是4．

Answer 1

分析 （1）作点P关于OA的对称点P′，作点P关于OB的对称点P″，连接P′P″分别OA于点Q交OB于点R，连接OP′，OP″（如图1所示），此时△PQR周长最小，根据全等三角形的判定定理可得出△P′AQ≌△PAQ、△POR=△P″OR，通过角的计算即可得出α、β之间的关系；
（2）根据一次函数的性质画出P关于x的图象，由此即可得出结论．

解答 解：（1）作点P关于OA的对称点P′，作点P关于OB的对称点P″，连接P′P″分别OA于点Q交OB于点R，连接OP′，OP″（如图1所示），此时△PQR周长最小，
∵点P、P′关于OA对称，点P、P″关于OB对称，
∴OP′=OP=OP″，∠P′AQ=∠PAQ，∠POR=∠P″OR，
在△P′AQ=△PAQ中，$\left\{\begin{array}{l}{OP′=OP}\\{∠P′OQ=∠POQ}\\{OQ=OQ}\end{array}\right.$，
∴△P′AQ≌△PAQ（SAS），
同理：△POR=△P″OR．
∴∠OPQ=∠OP′Q，∠OPR=∠OP″R．
在△P′OP″中，OP″=OP′，∠P′OP″=∠P′OQ+∠QOR+∠ROP″=2α，
∴β=∠OP′Q+∠OP″R=180°-∠P′OP″=180°-2α，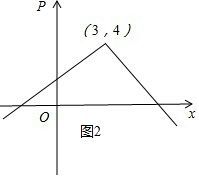
∴β+2α=180°．
故答案为：β+2α=180°．
（2）由题意可知：y₁=m₁x-3m₁+4，y₂=m₂x-3m₂+4．
∵m₁m₂＜0，
不失一般性，设m₁＜0＜m₂，
依照题意画出P关于x的函数图象，如图2所示．
结合函数图象可知P=4．
故答案为：4．

点评 本题考查了轴对称中的最短路线问题、一次函数的性质以及一次函数的图象，解题的关键是：（1）找出△PQR周长最小时点Q、R的位置；（2）画出P关于x的函数图象．本题属于中档题，难度不大，解决该题型题目时，根据找点的轴对称点确定Q、R点的位置是关键．