
ЁОЬтФПЁПШчЭМЃЈ1ЃЉЃЌЙЋТЗЩЯгаAЁЂBЁЂCШ§ИіГЕеОЃЌвЛСОЦћГЕДгAеОвдЫйЖШv1дШЫйЪЛЯђBеОЃЌЕНДяBеОКѓВЛЭЃСєЃЌвдЫйЖШv2дШЫйЪЛЯђCеОЃЌЦћГЕааЪЛТЗГЬyЃЈЧЇУзЃЉгыааЪЛЪБМфxЃЈаЁЪБЃЉжЎМфЕФКЏЪ§ЭМЯѓШчЭМЃЈ2ЃЉЫљЪОЃЎ

ЃЈ1ЃЉЕБЦћГЕдкAЁЂBСНеОжЎМфдШЫйааЪЛЪБЃЌЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНМАздБфСПЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЧѓГіv2ЕФжЕЃЛ
ЃЈ3ЃЉШєЦћГЕдкФГвЛЖЮТЗГЬФкИеКУгУ50ЗжжгааЪЛСЫ90ЧЇУзЃЌЧѓетЖЮТЗГЬПЊЪМЪБxЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=100xЃЌЃЈ0ЃМxЃМ3ЃЉЃЛЃЈ2ЃЉ120ЧЇУз/аЁЪБЃЛЃЈ3ЃЉетЖЮТЗГЬПЊЪМЪБxЕФжЕЪЧ2.5аЁЪБЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнКЏЪ§ЭМЯѓЩшГівЛДЮКЏЪ§НтЮіЪНЃЌдЫгУД§ЖЈЯЕЪ§ЗЈЧѓГіНтЮіЪНМДПЩЃЛ
ЃЈ2ЃЉИљОнОрРыЁТЪБМф=ЫйЖШМЦЫуЃЛ
ЃЈ3ЃЉЩшЦћГЕдкAЁЂBСНеОжЎМфдШЫйааЪЛxаЁЪБЃЌИљОнЬтвтСаГіЗНГЬЃЌНтЗНГЬМДПЩЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉИљОнЭМЯѓПЩЩшЦћГЕдкAЁЂBСНеОжЎМфдШЫйааЪЛЪБЃЌyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЮЊy=kxЃЌ
ЁпЭМЯѓОЙ§ЃЈ1ЃЌ100ЃЉЃЌ
Ёрk=100ЃЌ
ЁрyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЮЊy=100xЃЌЃЈ0ЃМxЃМ3ЃЉЃЛ
ЃЈ2ЃЉЕБy=300ЪБЃЌx=3ЃЌ
4Љ3=1аЁЪБЃЌ420Љ300=120ЧЇУзЃЌ
Ёрv2=120ЧЇУз/аЁЪБЃЛ
ЃЈ3ЃЉЩшЦћГЕдкAЁЂBСНеОжЎМфдШЫйааЪЛxаЁЪБЃЌдђдкЦћГЕдкBЁЂCСНеОжЎМфдШЫйааЪЛЃЈ![]() ЉxЃЉаЁЪБЃЌ
ЉxЃЉаЁЪБЃЌ
гЩЬтвтЕУЃЌ100x+120ЃЈ![]() ЉxЃЉ=90ЃЌ
ЉxЃЉ=90ЃЌ
НтЕУx=0.5ЃЌ
3Љ0.5=2.5аЁЪБЃЎ
Д№ЃКетЖЮТЗГЬПЊЪМЪБxЕФжЕЪЧ2.5аЁЪБЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌOЮЊзјБъдЕуЃЌЕуA(1ЃЌ5)КЭЕуB(mЃЌ1)ОљдкЗДБШР§КЏЪ§yЃН![]() ЭМЯѓЩЯЃЎ
ЭМЯѓЩЯЃЎ
(1)ЧѓmЃЌkЕФжЕЃЛ
(2)ЩшжБЯпABгыxжсНЛгкЕуCЃЌЧѓЁїAOCЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋБпГЄЮЊ![]() ЕФСтаЮABCDжНЦЌЗХжУдкЦНУцжБНЧзјБъЯЕжаЃЎвбжЊЁЯABO=45ЁуЃЎ
ЕФСтаЮABCDжНЦЌЗХжУдкЦНУцжБНЧзјБъЯЕжаЃЎвбжЊЁЯABO=45ЁуЃЎ
ЃЈ1ЃЉЧѓГіЕуBЁЂCЕФзјБъЃЛ
ЃЈ2ЃЉЩшБпABбиyжсЖделКѓЕФЖдгІЯпЖЮЮЊABЁфЃЌЧѓГіЕуBЁфЕФзјБъМАЯпЖЮCBЁфЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=ACЃЌЁЯBAC=90ЁуЃЌAHЁЭBCгкЕуHЃЌЙ§ЕуCзїCDЁЭACЃЌСЌНгADЃЌЕуMЮЊACЩЯвЛЕуЃЌЧвAM=CDЃЌСЌНгBMНЛAHгкЕуNЃЌНЛADгкЕуEЃЎ

ЃЈ1ЃЉШєAB=3ЃЌAD=![]() ЃЌЧѓЁїBMCЕФУцЛ§ЃЛ
ЃЌЧѓЁїBMCЕФУцЛ§ЃЛ
ЃЈ2ЃЉЕуEЮЊADЕФжаЕуЪБЃЌЧѓжЄЃКAD=![]() BN ЃЎ
BN ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯп![]() ЃЌЦфжа
ЃЌЦфжа![]() ЪЧГЃЪ§ЃЌИУХзЮяЯпЕФЖдГЦжсЮЊжБЯп
ЪЧГЃЪ§ЃЌИУХзЮяЯпЕФЖдГЦжсЮЊжБЯп![]() ЃЎ
ЃЎ
ЃЈ![]() ЃЉЧѓИУХзЮяЯпЕФКЏЪ§НтЮіЪНЃЎ
ЃЉЧѓИУХзЮяЯпЕФКЏЪ§НтЮіЪНЃЎ
ЃЈ![]() ЃЉАбИУХзЮяЯпби
ЃЉАбИУХзЮяЯпби![]() жсЯђЩЯЦНвЦЖрЩйИіЕЅЮЛКѓЃЌЕУЕНЕФХзЮяЯпгы
жсЯђЩЯЦНвЦЖрЩйИіЕЅЮЛКѓЃЌЕУЕНЕФХзЮяЯпгы![]() жсжЛгавЛИіЙЋЙВЕуЃЎ
жсжЛгавЛИіЙЋЙВЕуЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
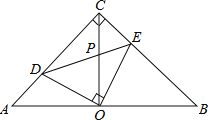
ЁОЬтФПЁПШчЭМЃЌдкЕШбќжБНЧЁїABCжаЃЌЁЯACB=90ЁуЃЌOЪЧаББпABЕФжаЕуЃЌЕуDЃЌEЗжБ№дкжБНЧБпACЃЌBCЩЯЃЌЧвЁЯDOE=90ЁуЃЌDEНЛOCгкЕуPЃЎдђЯТСаНсТлЃК(1)AD+BE=ACЃЛ(2)AD2+BE2=DE2ЃЛ(3)ЁїABCЕФУцЛ§ЕШгкЫФБпаЮCDOEУцЛ§ЕФ2БЖЃЛ(4)OD=OEЃЎЦфжае§ШЗЕФНсТлга( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌЕуDЮЊБпBCЩЯвЛЕуЃЌЧыЛиД№ЯТСаЮЪЬтЃК

ЃЈ1ЃЉШчЭМ1ЃЌШєЁЯDAC=ЁЯBЃЌЁїABCЕФНЧЦНЗжЯпCEНЛADгкЕуFЃЌЪдЫЕУїЁЯAEF=ЁЯAFEЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌШчЭМ2ЃЌЁїABCЕФЭтНЧЁЯACQЕФНЧЦНЗжЯпCPНЛBAЕФбгГЄЯпгкЕуPЃЌШєЁЯP=26ЁуЃЌВТЯыЁЯCFDЕФЖШЪ§ЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDжаЃЌEЁЂFЗжБ№ЪЧБпADЁЂCDЩЯЕФЕуЃЌAE=EDЃЌDF=![]() DCЃЌСЌНгEFВЂбгГЄНЛBCЕФбгГЄЯпгкЕуGЁЃ
DCЃЌСЌНгEFВЂбгГЄНЛBCЕФбгГЄЯпгкЕуGЁЃ
ЃЈ1ЃЉЧѓжЄЃКЁїABEЁзЁїDEFЃЛ
ЃЈ2ЃЉШєе§ЗНаЮЕФБпГЄЮЊ4ЃЌЧѓBGЕФГЄЁЃ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯп![]() ЃК
ЃК![]() КЭжБЯп
КЭжБЯп![]() ЃК
ЃК![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() жсЃЌНЛжБЯп
жсЃЌНЛжБЯп![]() гкЕуAЃЌШєЕуPЪЧxжсЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуPзїЦНаагкyжсЕФжБЯпЃЌЗжБ№гы
гкЕуAЃЌШєЕуPЪЧxжсЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуPзїЦНаагкyжсЕФжБЯпЃЌЗжБ№гы![]() ЁЂ
ЁЂ![]() НЛгкЕуCЁЂDЃЌСЌНгADЁЂBCЃЎ
НЛгкЕуCЁЂDЃЌСЌНгADЁЂBCЃЎ
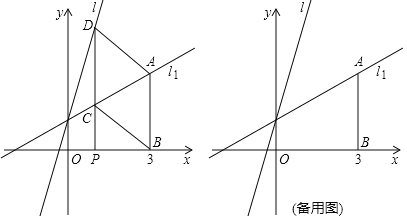
![]() жБНгаДГіЯпЖЮ
жБНгаДГіЯпЖЮ![]() ______ЃЛ
______ЃЛ
![]() ЕБPЕФзјБъЪЧ
ЕБPЕФзјБъЪЧ![]() ЪБЃЌЧѓжБЯпBCЕФНтЮіЪНЃЛ
ЪБЃЌЧѓжБЯпBCЕФНтЮіЪНЃЛ
![]() Шє
Шє![]() ЕФУцЛ§гы
ЕФУцЛ§гы![]() ЕФУцЛ§ЯрЕШЃЌЧѓЕуPЕФзјБъЃЎ
ЕФУцЛ§ЯрЕШЃЌЧѓЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com