
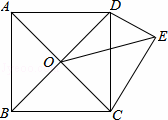
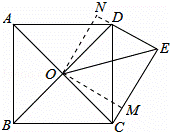
如图,ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,∠DCE=30°,若OE=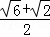 ,则正方形的面积为( )
,则正方形的面积为( )
|
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
B
解:如图,过点O作OM⊥CE于M,作ON⊥DE交ED的延长线于N,
∵∠CED=90°,
∴四边形OMEN是矩形,
∴∠MON=90°,
∵∠COM+∠DOM=∠DON+∠DOM,
∴∠COM=∠DON,
∵四边形ABCD是正方形,
∴OC=OD,
在△COM和△DON中,
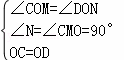 ,
,
∴△COM≌△DON(AAS),
∴OM=ON,
∴四边形OMEN是正方形,
设正方形ABCD的边长为2a,则OC=OD=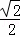 ×2a=
×2a= a,
a,
∵∠CED=90°,∠DCE=30°,
∴DE=CD=a,
由勾股定理得,CE=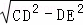 =
=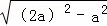 =
=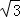 a,
a,
∴四边形OCED的面积=a•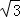 a+•(
a+•(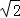 a)•(
a)•(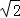 a)=×(
a)=×(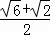 )2,
)2,
解得a2=1,
所以,正方形ABCD的面积=(2a)2=4a2=4×1=4.
故选B.


 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是双曲线y=(x>0)上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )

|
| A. | 逐渐增大 | B. | 不变 | C. | 逐渐减小 | D. | 先增大后减小 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,抛物线y=ax2+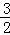 x+c与x轴交于点A(4,0)、B(﹣1,0),与y轴交于点C,连接AC,点M是线段OA上的一个动点(不与点O、A重合),过点M作MN∥AC,交OC于点N,将△OMN沿直线MN折叠,点O的对应点O′落在第一象限内,设OM=t,△O′MN与梯形AMNC重合部分面积为S.
x+c与x轴交于点A(4,0)、B(﹣1,0),与y轴交于点C,连接AC,点M是线段OA上的一个动点(不与点O、A重合),过点M作MN∥AC,交OC于点N,将△OMN沿直线MN折叠,点O的对应点O′落在第一象限内,设OM=t,△O′MN与梯形AMNC重合部分面积为S.
(1)求抛物线的解析式;
(2)①当点O′落在AC上时,请直接写出此时t的值;
②求S与t的函数关系式;
(3)在点M运动的过程中,请直接写出以O、B、C、O′为顶点的四边形分别是等腰梯形和平行四边形时所对应的t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,⊙O的直径CD垂直于弦AB,垂足为E,F为DC延长线上一点,且∠CBF=∠CDB.
(1)求证:FB为⊙O的切线;
(2)若AB=8,CE=2,求sin∠F.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com