Question

如图,抛物线y=ax²+bx+c与x轴的一个交点A的坐标为（﹣1，0），对称轴为直线x=﹣2．

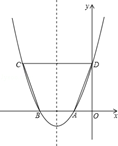
（1）求抛物线与x轴的另一个交点B的坐标；

（2）点D是抛物线与y轴的交点，点C是抛物线上的另一点．若以AB为一底边的梯形ABCD的面积为9．

求此抛物线的解析式，并指出顶点E的坐标；

（3）点P是（2）中抛物线对称轴上一动点，且以1个单位/秒的速度从此抛物线的顶点E向上运动．设点P运动的时间为t秒．

①当t为　  　秒时，△PAD的周长最小？当t为      秒时，△PAD是以AD为腰的等腰三角形？（结果保留根号）

②点P在运动过程中，是否存在一点P，使△PAD是以AD为斜边的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．

 

Answer 1

【答案】

（1） B（﹣3，0）；

（2）y=x²+4x+3化为顶点式为y=（x+2）²﹣1，得E（﹣2，﹣1）；

（3）①2；4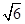或4﹣或4+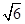;  ②存在一点P，使△PAD是以AD为斜边的直角三角形, P（﹣2，1）或（﹣2，2）．

【解析】

试题分析：（1）根据抛物线的轴对称性可得抛物线与x轴的另一个交点B的坐标；

（2）先根据梯形ABCD的面积为9，可求c的值，再运用待定系数法可求抛物线的解析式，转化为顶点式可求顶点E的坐标；

（3）①根据轴对称﹣最短路线问题的求法可得△PAD的周长最小时t的值；根据等腰三角形的性质可分三种情况求得△PAD是以AD为腰的等腰三角形时t的值；

②先证明△APN∽△PDM，根据相似三角形的性质求得PN的值，从而得到点P的坐标．

试题解析：（1）由抛物线的轴对称性及A（﹣1，0），可得B（﹣3，0）；

（2）设抛物线的对称轴交CD于点M，交AB于点N，

由题意可知AB∥CD，由抛物线的轴对称性可得CD=2DM．

∵MN∥y轴，AB∥CD，

∴四边形ODMN是矩形．

∴DM=ON=2，

∴CD=2×2=4．

∵A（﹣1，0），B（﹣3，0），

∴AB=2，

∵梯形ABCD的面积=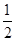（AB+CD）•OD=9，

∴OD=3，即c=3．

∴把A（﹣1，0），B（﹣3，0）代入y=ax²+bx+3得，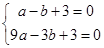

解得．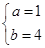

∴y=x²+4x+3．

将y=x²+4x+3化为顶点式为y=（x+2）²﹣1，得E（﹣2，﹣1）；

（3）①当t为2秒时，△PAD的周长最小；当t为4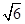或4﹣或4+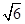秒时，△PAD是以AD为腰的等腰三角形．

故答案为：2；4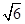或4﹣或4+．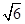

②存在．

∵∠APD=90°，∠PMD=∠PNA=90°，

∴∠DPM+∠APN=90°，∠DPM+∠PDM=90°，

∴∠PDM=∠APN，

∵∠PMD=∠ANP，

∴△APN∽△PDM，

∴，

∴，

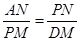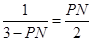∴PN²﹣3PN+2=0，

∴PN=1或PN=2．

∴P（﹣2，1）或（﹣2，2）．

考点：二次函数综合题．