
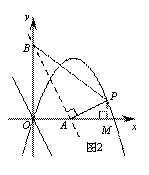
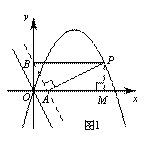
如图,已知点P是二次函数y=-x2+3x图象在y轴右侧部分上的一个动点,将直线y=-2x沿y轴向上平移,分别交x轴、y轴于A、B两点. 若以AB为直角边的△PAB与△OAB相似,请求出所有符合条件的点P的坐标.
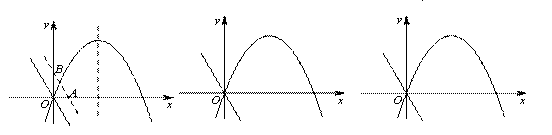 |
解:由题意,设OA=m,则OB=2m;当∠BAP=90°时,
△BAP∽△AOB或△BAP∽△BOA;
① 若△BAP∽△AOB,如图1,
可知△PMA∽△AOB,相似比为2:1;则P1(5m,2m),
代入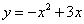 ,可知
,可知 ,
,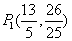
② 若△BAP∽△BOA,如图2,
可知△PMA∽△AOB,相似比为1:2;则P2(2m, ),
),
代入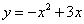 ,可知
,可知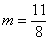 ,
,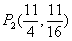
当∠ABP=90°时,△ABP∽△AOB或△ABP∽△BOA;
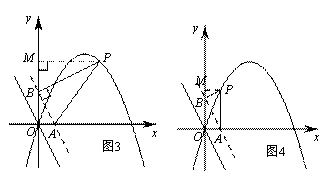
③ 若△ABP∽△AOB,如图3,
可知△PMB∽△BOA,相似比为2:1;则P3(4m,4m),
代入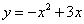 ,可知
,可知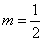 ,
,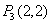
④ 若△ABP∽△BOA,如图4,
可知△PMB∽△BOA,相似比为1:2;则P4(m,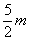 ),
),
 代入
代入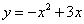 ,可知
,可知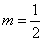 ,
,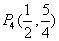
 |  | ||


科目:初中数学 来源: 题型:
点A,B在同一直线上,A到直线a离为7cm,点B到直线 a距离为3cm,则线段AB的长度为 ( )
a距离为3cm,则线段AB的长度为 ( )
A.10cm或4cm B.4cm C.10cm D.至少4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
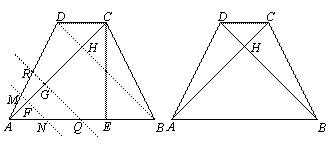
如图,等腰梯形ABCD中,AB∥CD,AB= , CD=
, CD=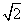 ,高CE=
,高CE=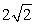 ,对角线AC、BD交于点H.平行于线段BD的两条直线MN、RQ同时从点A出发,沿AC方向向点C匀速平移,分别交等腰梯形ABCD的边于M、N和R、Q,分别交对角线AC于F、G,当直线RQ到达点C时,两直线同时停止移动.记等腰梯形ABCD被直线MN扫过的面积为
,对角线AC、BD交于点H.平行于线段BD的两条直线MN、RQ同时从点A出发,沿AC方向向点C匀速平移,分别交等腰梯形ABCD的边于M、N和R、Q,分别交对角线AC于F、G,当直线RQ到达点C时,两直线同时停止移动.记等腰梯形ABCD被直线MN扫过的面积为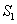 ,被直线RQ扫过的面积为
,被直线RQ扫过的面积为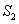 ,若直线MN平移的速度为1单位/秒,直线RQ平移的速度为2单位/秒,设两直线移动的时间为x秒.
,若直线MN平移的速度为1单位/秒,直线RQ平移的速度为2单位/秒,设两直线移动的时间为x秒.
(1)填空:∠AHB=____________;AC=_____________;
(2)若 ,求x.
,求x.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
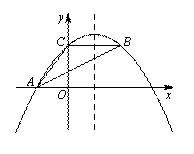
如图,抛物线y=ax2-5ax+4(a<0)经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.
(1)求抛物线的解析式.
(2)在抛物线的对称轴上是否存在点M,使|MA-MB|最大?
若存在,求出点M的坐标;若不存在,请说明理由.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
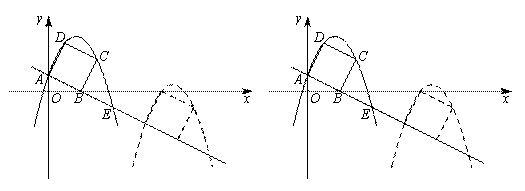
如图,已知直线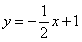 与坐标轴交于A,B两点,以线段AB为边向上作正方形ABCD,过点A,D,C的抛物线与直线的另一个交点为E.
与坐标轴交于A,B两点,以线段AB为边向上作正方形ABCD,过点A,D,C的抛物线与直线的另一个交点为E.
(1)请直接写出C,D两点的坐标,并求出抛物线的解析式;
(2)若正方形以每秒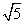 个单位长度的速度沿射线AB下滑,直至顶点D落在x轴上时停止,设正方形落在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围;
个单位长度的速度沿射线AB下滑,直至顶点D落在x轴上时停止,设正方形落在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围;
(3)在(2)的条件下,抛物线与正方形一起平移,同时停止,求抛物线上C,E两点间的抛物线弧所扫过的面积.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
已知w关于t的函数: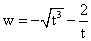 ,则下列有关此函数图像的描述正确的是( )
,则下列有关此函数图像的描述正确的是( )
(A)该函数图像与坐标轴有两个交点 (B)该函数图像经过第一象限
(C)该函数图像关于原点中心对称 (D)该函数图像在第四象限
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com