
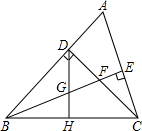
 已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH与BE相交于点G.
已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH与BE相交于点G.分析 (1)欲证明AC=BF,只要证明△ADC≌△FDB即可.
(2)只要证明BA=BC,根据等腰三角形的性质(三线合一),可知AE=EC=$\frac{1}{2}$AC=$\frac{1}{2}$BF.
(3)由DGF=∠DBG+∠BDG=67.5°,∠DFG=∠FBC+∠BCF=67.5°,推出∠DGF=∠DFG,即可证明.
解答 证明:(1)∵∠ABC=45°,CD⊥AB于D,
∴∠DBC=∠DCB=45°,
∴DB=DC,
∵BE⊥AC,
∴∠AEB=∠ADC=90°,
∴∠A+∠ABE=90°,∠A+ACD=90°,
∴∠DBF=∠ACD,
在△ADC和△FDB中,
$\left\{\begin{array}{l}{∠ACD=∠DBF}\\{DC=BD}\\{∠ADC=∠BDF=90°}\end{array}\right.$,
∴△ADC≌△FDB,
∴AC=BF.
(2)∵∠ABE=∠CBE,∠ABE+∠A=90°,∠CBE+∠BCA=90°,
∴∠A=∠BCA,
∴BA=BC,
∵BE⊥AC,
∴AE=CE,
∵AC=BF,
∴CE=$\frac{1}{2}$BF.
(3)∵DB=DC,∠BDC=90°,BH=CH,
∴DH⊥BC,
∴DH=BH=HC,
∴∠HDB=∠HBD=∠BCD=45°,
∵∠FBD=∠FBC=22.5°,
∴∠DGF=∠DBG+∠BDG=67.5°,∠DFG=∠FBC+∠BCF=67.5°,
∴∠DGF=∠DFG,
∴DG=DF.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质、线段的垂直平分线的性质等知识,解题的关键是正确寻找全等三角形解决问题,灵活运用所学知识,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
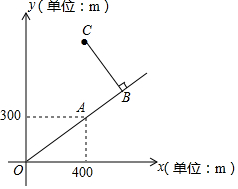 如图是根据某公园的平面示意图建立的平面直角坐标,公园的入口位于坐标原点,古塔位于点A(400,300).从古塔出发沿线OA方向前进300m是盆景园B,从盆景园B向左转90°后直行400m到达梅花阁C,则点C坐标是( )
如图是根据某公园的平面示意图建立的平面直角坐标,公园的入口位于坐标原点,古塔位于点A(400,300).从古塔出发沿线OA方向前进300m是盆景园B,从盆景园B向左转90°后直行400m到达梅花阁C,则点C坐标是( )| A. | (300,800) | B. | (400,500) | C. | (300,500) | D. | (400,800) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
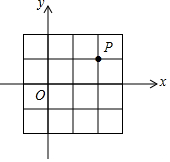 如图,在平面直角坐标系中,将点P(2,1)向下平移3个单位长度,再向左平移1个单位长度得到点Q,则点Q的坐标为( )
如图,在平面直角坐标系中,将点P(2,1)向下平移3个单位长度,再向左平移1个单位长度得到点Q,则点Q的坐标为( )| A. | (3,-2) | B. | (-1,-2) | C. | (1,-2) | D. | (0,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知扇形纸片OEF,∠EOF=120°,点P是弧$\widehat{EF}$上任意点(不与E、F重合),连结PE、PF,折叠纸片,使E、F都与点P重合,折痕OA、OB分别与PE、PF交于点M、N,若MN=$\sqrt{3}$,则扇形OAB的面积是( )
已知扇形纸片OEF,∠EOF=120°,点P是弧$\widehat{EF}$上任意点(不与E、F重合),连结PE、PF,折叠纸片,使E、F都与点P重合,折痕OA、OB分别与PE、PF交于点M、N,若MN=$\sqrt{3}$,则扇形OAB的面积是( )| A. | $\frac{1}{3}$π | B. | $\frac{2}{3}$π | C. | π | D. | $\frac{4}{3}$π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
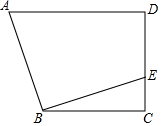 如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD=8,过点B作EB⊥AB,交CD于点E.若DE=6,则AD的长为( )
如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD=8,过点B作EB⊥AB,交CD于点E.若DE=6,则AD的长为( )| A. | 6 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com