
【题目】如图,抛物线![]() (
(![]() )与y轴交于点A,与x轴交于B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4,现将抛物线沿BA方向平移,平移后的抛物线过点C时,与x轴的另一点为E,其顶点为F,对称轴与x轴的交点为H.
)与y轴交于点A,与x轴交于B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4,现将抛物线沿BA方向平移,平移后的抛物线过点C时,与x轴的另一点为E,其顶点为F,对称轴与x轴的交点为H.
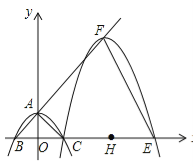
(1)求a、c的值及抛物线的解析式.
(2)连接OF,试判断△OEF是否为等腰三角形,并说明理由.
【答案】(1)a=![]() ,c=2;(2)△OEF是等腰三角形.
,c=2;(2)△OEF是等腰三角形.
【解析】
试题分析:(1)由A(0,c),得到OA=c,再由等腰直角三角形的性质得OA=OB=OC=c,由三角形面积公式解得![]() ,解得c=2,把C(2,0)代入
,解得c=2,把C(2,0)代入![]() 可求出a的值;
可求出a的值;
(2)如图1,先利用待定系数法求出直线AB的解析式为![]() ,设F(t,t+2),利用抛物线平移的规律可设平移后的抛物线解析式为
,设F(t,t+2),利用抛物线平移的规律可设平移后的抛物线解析式为![]() ,再把C(2,0)代入
,再把C(2,0)代入![]() 解得t=6,则平移后的抛物线解析式为
解得t=6,则平移后的抛物线解析式为![]() ,所以F(6,8),利用勾股定理得出OF=10,由抛物线与x轴的交点确定E(10,0),则OE=OF=10,于是可判断△OEF为等腰三角形;
,所以F(6,8),利用勾股定理得出OF=10,由抛物线与x轴的交点确定E(10,0),则OE=OF=10,于是可判断△OEF为等腰三角形;
试题解析:解:(1)∵抛物线![]() (
(![]() )与y轴交于点A,
)与y轴交于点A,
∴A(0,c),则OA=c,
∵△ABC为等腰直角三角形,
∴OA=OB=OC=c,
∴![]() c2c=4,解得c=2,
c2c=4,解得c=2,
∴C(2,0),
把C(2,0)代入![]() 得4a+2=0,解得a=
得4a+2=0,解得a=![]() ;
;
抛物线的解析式是:![]() .
.
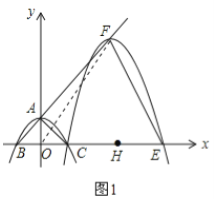
(2)△OEF是等腰三角形.理由如下:如图1,
设直线AB的解析式为![]() ,
,
把A(0,2)、B(﹣2,0)代入得![]() ,解得:
,解得:![]() ,
,
则直线AB的解析式为![]() ,设F(t,t+2),
,设F(t,t+2),
∵抛物线![]() 沿BA方向平移,平移后的抛物线过点C时,顶点为F,
沿BA方向平移,平移后的抛物线过点C时,顶点为F,
∴平移后的抛物线解析式为![]() ,
,
把C(2,0)代入得![]() ,解得t=6,
,解得t=6,
∴平移后的抛物线解析式为![]() ,
,
∴F(6,),
∴OF=![]() =10,
=10,
令y=0时,![]() ,解得
,解得![]() ,
,![]() ,
,
∴OE=10,
∴OE=OF,
∴△OEF为等腰三角形;


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】从多边形一条边上的一点(不是顶点)出发,连接各个顶点得到2 013个三角形,则这个多边形的边数为( )
A. 2 011 B. 2 015 C. 2 014 D. 2 016
查看答案和解析>>
科目:初中数学 来源: 题型:
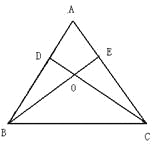
【题目】已知:如图,锐角△ABC的两条高BE、CD相交于点O,且OB=OC,
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的角平分线上,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系xOy中,反比例函数y1=![]() (x>0)的图象与一次函数y2=kx-k的图象的交点为A(m,2).
(x>0)的图象与一次函数y2=kx-k的图象的交点为A(m,2).
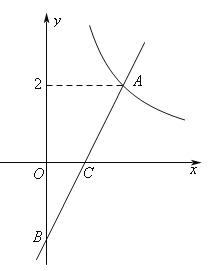
(1)求一次函数的解析式;
(2)观察图像,直接写出使y1≥y2的x的取值范围.
(3)设一次函数y=kx-k的图象与y轴交于点B,若点P是x轴上一点,且满足△PAB的面积是4,请写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)居民区内的“广场舞”引起媒体关注,小王想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:A.非常赞同;B.赞同但要有时间限制;C.无所谓;D.不赞同.并将调查结果绘制了图1和图2两幅不完整的统计图.
请你根据图中提供的信息解答下列问题:

(1)求本次被抽查的居民有多少人?
(2)将图1和图2补充完整;
(3)求图2中“C”层次所在扇形的圆心角的度数;
(4)估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,BCE、AFE是直线,AB∥CD,∠1=∠2,∠3=∠4.AD与BE平行吗?为什么?
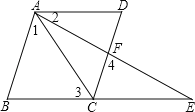
解:AD∥BE,理由如下:
∵AB∥CD(已知)
∴∠4= ( )
∵∠3=∠4(已知)
∴∠3= ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF( )
即 =
∴∠3= ( )
∴AD∥BE( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com