
【题目】请完成下面的几何探究过程:
(1)观察填空
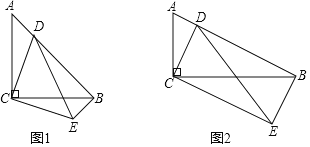
如图1,在Rt△ABC中,∠C=90°,AC=BC=4,点D为斜边AB上一动点(不与点A,B重合),把线段CD绕点C顺时针旋转90°得到线段CE,连DE,BE,则
①∠CBE的度数为____________;
②当BE=____________时,四边形CDBE为正方形.
(2)探究证明
如图2,在Rt△ABC中,∠C=90°,BC=2AC=4,点D为斜边AB上一动点(不与点A,B重合),把线段CD绕点C顺时针旋转90°后并延长为原来的两倍得到线段CE,连DE,BE则:
①在点D的运动过程中,请判断∠CBE与∠A的大小关系,并证明;
②当CD⊥AB时,求证:四边形CDBE为矩形
(3)拓展延伸
如图2,在点D的运动过程中,若△BCD恰好为等腰三角形,请直接写出此时AD的长.
【答案】(1)①45°,②![]() ;(2)①
;(2)①![]() ,理由见解析,②见解析;(3)
,理由见解析,②见解析;(3)![]() 或
或![]()
【解析】
(1)①由等腰直角三角形的性质得出![]() ,由旋转的性质得:
,由旋转的性质得:![]() ,
,![]() ,证明
,证明![]() ,即可得出结果;
,即可得出结果;
②由①得![]() ,求出
,求出![]() ,作
,作![]() 于
于![]() ,则
,则![]() 是等腰直角三角形,证出
是等腰直角三角形,证出![]() 是等腰直角三角形,求出
是等腰直角三角形,求出![]() ,证出四边形
,证出四边形![]() 是矩形,再由垂直平分线的性质得出
是矩形,再由垂直平分线的性质得出![]() ,即可得出结论;
,即可得出结论;
(2)①证明![]() ,即可得出
,即可得出![]() ;
;
②由垂直的定义得出![]() ,由相似三角形的性质得出
,由相似三角形的性质得出![]() ,即可得出结论;
,即可得出结论;
(3)存在两种情况:①当![]() 时,证出
时,证出![]() ,由勾股定理求出
,由勾股定理求出![]() ,即可得出结果;
,即可得出结果;
②当![]() 时,得出
时,得出![]() 即可.
即可.
解:(1)①![]() ,
,![]() ,
,
![]() ,
,
由旋转的性质得:![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,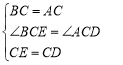 ,
,
![]() ,
,
![]() ;
;
故答案为:![]() ;
;
②当![]() 时,四边形
时,四边形![]() 是正方形;理由如下:
是正方形;理由如下:
由①得:![]() ,
,
![]() ,
,
作![]() 于
于![]() ,如图所示:
,如图所示:

则![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,
又![]() 垂直平分
垂直平分![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是正方形;
是正方形;
故答案为:![]() ;
;
(2)①![]() ,理由如下:
,理由如下:
由旋转的性质得:![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ;
;
②![]() ,
,
![]() ,
,
由①得:![]() ,
,
![]() ,
,
又![]() ,
,
![]() 四边形
四边形![]() 是矩形;
是矩形;
(3)在点![]() 的运动过程中,若
的运动过程中,若![]() 恰好为等腰三角形,存在两种情况:
恰好为等腰三角形,存在两种情况:
①当![]() 时,则
时,则![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
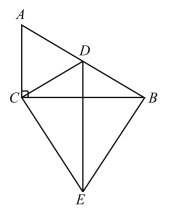
②当![]() 时,
时,![]() ;
;
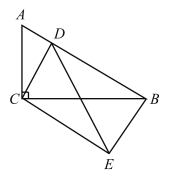
综上所述:若![]() 恰好为等腰三角形,此时
恰好为等腰三角形,此时![]() 的长为
的长为![]() 或
或![]() .
.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
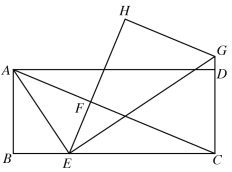
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是对角线,点
是对角线,点![]() 在线段
在线段![]() 上,连结
上,连结![]() ,将
,将![]() 沿
沿![]() 翻折,使得点
翻折,使得点![]() 的对应点
的对应点![]() 恰好落在
恰好落在![]() 上,点
上,点![]() 在射线
在射线![]() 上,连接
上,连接![]() ,将
,将![]() 沿
沿![]() 翻折,使得点
翻折,使得点![]() 的对应点
的对应点![]() 恰好落在
恰好落在![]() 所在直线,则线段
所在直线,则线段![]() 的长度为( )
的长度为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次课题学习中,老师让同学们合作编题,某学习小组受赵爽弦图的启发,编写了下面这道题,请你来解一解:如图,将平行四边形ABCD的四边DA、AB、BC、CD分别延长至E、F、G、H,使得AE=CG,BF=DH,连接EF,FG,GH,HE.求证:四边形EFGH为平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干学生的兴趣爱好;并将调查的结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
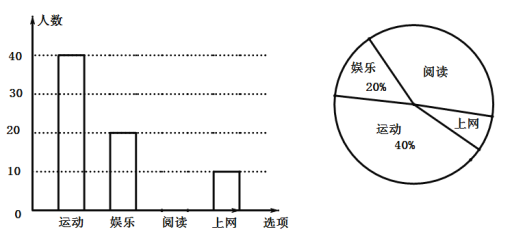
(1)在这次研究中,一共调查了______名学生;若该校共有1500名学生,估计全校爱好运动的学生共有______名;
(2)补全条形统计图,并计算阅读部分圆心角是______度;
(3)若该校九年级爱好阅读的学生有150人,估计九年级有多少学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
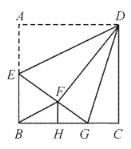
【题目】如图,正方形![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,
,![]() ,垂足为
,垂足为![]() ,连接
,连接![]() 、
、![]() .结论:①
.结论:①![]() ;②
;②![]() ≌
≌![]() ;③
;③![]() ∽
∽![]() ;④
;④![]() ;⑤
;⑤![]() .其中的正确的个数是( )
.其中的正确的个数是( )
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,抛物线的对称轴是直线
,抛物线的对称轴是直线![]() .
.
(1)求抛物线对应的函数表达式;
(2)![]() 是线段
是线段![]() 上的任意一点,当
上的任意一点,当![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标.
的坐标.
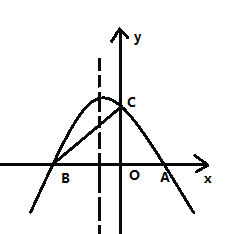
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4张相同的卡片分别写有数字﹣1、﹣3、4、6,将这些卡片的背面朝上,并洗匀.
(1)从中任意抽取1张,抽到的数字大于0的概率是______;
(2)从中任意抽取1张,并将卡片上的数字记作二次函数y=ax2+bx中的a,再从余下的卡片中任意抽取1张,并将卡片上的数字记作二次函数y=ax2+bx中的b,利用树状图或表格的方法,求出这个二次函数图象的对称轴在y轴右侧的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com