
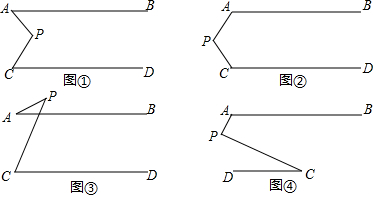
·ÖĪö £Ø1£©ŅĄ¾Ż”ĻAPC=m£¬”ĻPAB=n£¬”ĻPCD=t£¬Š“³ö”ĻAPCŗĶ”ĻPAB”¢”ĻPCDµÄŹżĮæ¹ŲĻµ£®
£Ø2£©Ķ¼¢ŁÖŠ£¬×÷PE”ĪAB£»Ķ¼¢ŚÖŠ£¬×÷PF”ĪAB£»Ķ¼¢ŪÖŠŌĖÓĆČż½ĒŠĪĶā½ĒŠŌÖŹ£»Ķ¼¢ÜÖŠ£¬×÷PH”ĪAB£¬·Öøł¾ŻĘ½ŠŠĻߵĊŌÖŹ½ųŠŠĶʵ¼¼ĘĖć¼“æÉµĆ³ö½įĀŪ£®
½ā“š 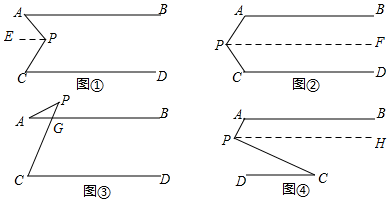 ½ā£ŗ£Ø1£©Ķ¼¢Ł£ŗm=n+t
½ā£ŗ£Ø1£©Ķ¼¢Ł£ŗm=n+t
Ķ¼¢Ś£ŗm+n+t=360”ćĶ¼¢Ū£ŗm+n=t
Ķ¼¢Ü£ŗm-t+n=180”ć
¹Ź“š°øĪŖ£ŗm=n+t£¬m+n+t=360”ć£¬m+n=t£¬m-t+n=180”ć£»
£Ø2£©ČōŃ”Ķ¼¢Ł£¬
¹żP×÷PE”ĪAB£¬ŌņPE”ĪCD£¬
”ą”ĻA=”ĻAPE=n£¬”ĻC=”ĻCPE=t£¬
”ą”ĻAPC=”ĻAPE+”ĻCPE=”ĻA+”ĻC£¬¼“m=n+t£»
ČōŃ”Ķ¼¢Ś£¬
¹żP×÷PF”ĪAB£¬ŌņPF”ĪCD£¬
”ą”ĻA+”ĻAPF=180”ć£¬”ĻC+”ĻCPF=180”ć£¬
”ą”ĻA+”ĻAPF+”ĻC+”ĻCPF=180”ć”Į2=360”ć£¬
¼“”ĻA+”ĻAPC+”ĻC=360”ć£¬
”ąm+n+t=360”ć£»
ČōŃ”Ķ¼¢Ū£¬
”ßAB”ĪCD£¬
”ą”ĻPGB=”ĻC£¬
Ó֔ߔĻPGB=”ĻA+”ĻAPC£¬
”ą”ĻC=”ĻA+”ĻAPC£¬¼“m+n=t£»
ČōŃ”Ķ¼¢Ü£¬
¹żP×÷PH”ĪAB£¬ŌņPH”ĪCD£¬
”ą”ĻA+”ĻAPH=180”ć£¬”ĻC=”ĻCPH=t£¬
Ó֔ߔĻAPH=”ĻAPC-”ĻCPH=m-t£¬
”ąn+m-t=180”ć£®
µćĘĄ ±¾ĢāÖ÷ŅŖæ¼²é¶ŌĘ½ŠŠĻߵĊŌÖŹ£¬Ę½ŠŠ¹«ĄķµÄĶĘĀŪ£¬Čż½ĒŠĪµÄĶā½ĒŠŌÖŹµČÖŖŹ¶µćµÄ×ŪŗĻÓ¦ÓĆ£¬ÄÜĮé»īŌĖÓĆŠŌÖŹ½ųŠŠĶĘĄķŹĒ½ā“ĖĢāµÄ¹Ų¼ü£®


 ĆūŠ£æĪĢĆĻµĮŠ“š°ø
ĆūŠ£æĪĢĆĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
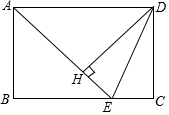 ČēĶ¼£¬ŌŚ¾ŲŠĪABCDÖŠ£¬AD=$\sqrt{2}$AB£¬”ĻBADµÄĘ½·ÖĻß½»BCÓŚµćE£¬DH”ĶAEÓŚµćH£¬Į¬½ÓDE£¬ĻĀĮŠ½įĀŪ£ŗ¢Ł”ĻAED=”ĻCED£»¢Ś”÷AEDĪŖµČŃüČż½ĒŠĪ£»¢ŪEH=CE£»¢ÜĶ¼ÖŠÓŠ3øöµČŃüČż½ĒŠĪ£®½įĀŪÕżČ·µÄøöŹżĪŖ£Ø””””£©
ČēĶ¼£¬ŌŚ¾ŲŠĪABCDÖŠ£¬AD=$\sqrt{2}$AB£¬”ĻBADµÄĘ½·ÖĻß½»BCÓŚµćE£¬DH”ĶAEÓŚµćH£¬Į¬½ÓDE£¬ĻĀĮŠ½įĀŪ£ŗ¢Ł”ĻAED=”ĻCED£»¢Ś”÷AEDĪŖµČŃüČż½ĒŠĪ£»¢ŪEH=CE£»¢ÜĶ¼ÖŠÓŠ3øöµČŃüČż½ĒŠĪ£®½įĀŪÕżČ·µÄøöŹżĪŖ£Ø””””£©| A£® | 1øö | B£® | 2øö | C£® | 3øö | D£® | 4øö |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | x1=0£¬x2=3 | B£® | x1=1£¬x2=-3 | C£® | x1=3£¬x2=7 | D£® | x1=-7£¬x2=-3 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
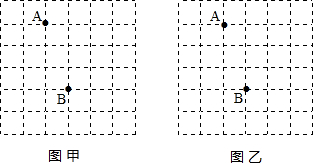
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 0»ņ3 | B£® | 0»ņ-3 | C£® | -3 | D£® | 3 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā

| A£® | 4øö | B£® | 3øö | C£® | 2øö | D£® | 1øö |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com