Question

“十一黄金周”的某一天，小刚全家上午8时自驾小汽车从家里出发，到距离180千米的某著名旅游景点游玩，该小汽车离家的路程S(千米)与时间t (时)的关系可以用右图的折线表示。根据图象提供的有关信息，解答下列问题：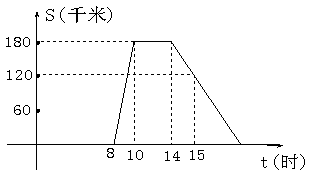

（1）小刚全家在旅游景点游玩了多少小时？
（2）求出整个旅程中S(千米)与时间t (时)的函数关系式，并求出相应自变量t的取值范围。
（3）小刚全家在什么时候离家120㎞？什么时候到家？

Answer 1

（1）4；（2）s=90t-720（8≤t≤10），s=180（10≤t≤14），s=-60t+1020（14≤t）；（3）9时20分或15时，t=17．

解析试题分析：（1）根据图示，在旅游景点停留的时间可以知道游玩的时间．
（2）根据图象信息可以得出整个旅程中S（千米）与时间t （时）的函数关系式，讨论实际情况得到t的取值范围．
（3）从图中信息可知当t=8时，S=0，当t=10时，S=180，可算出去时距离120km时的时间，由图可知回来时当t=15时，S=120km．根据回来时的函数可得到家的时间．
试题解析：（1）由图示信息可知，在距离180千米的某著名旅游景点游玩，停留了4小时，所以游玩了14-10=4小时
（2）当8≤t≤10时
设s=kt+b过点（8，0），（10，180）
得s=90t-720．
当10≤t≤14时
s=180
当14≤t时
过点（14，180），（15，120）得
∴s=90t-720（8≤t≤10）
s=180（10≤t≤14）
s=-60t+1020（14≤t）
（3）当s=120km时，
90t-720=120得t=9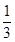
即9时20分
-60t+1020=120得t=15．
当s=0时
-60t+1020=0得t=17．
答：9时20分或15时离家120㎞，17时到家。
考点：一次函数的应用．