
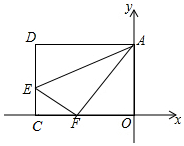
 如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处,若点D的坐标为(-10,8),则△AEF的面积为( )
如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处,若点D的坐标为(-10,8),则△AEF的面积为( )| A. | 15 | B. | 20 | C. | 25 | D. | 30 |
分析 根据折叠的性质得到AF=AD,所以在直角△AOF中,利用勾股定理求OF=6,然后设EC=x,则EF=DE=8-x,CF=10-6=4,根据勾股定理列方程求出EC,即可得到EF的长,最后计算△AEF的面积即可.
解答  解:∵四边形AOCD为矩形,D的坐标为(-10,8),
解:∵四边形AOCD为矩形,D的坐标为(-10,8),
∴AD=CO=10,DC=AO=8,
∵矩形沿AE折叠,使D落在CO上的点F处,
∴AD=AF=10,DE=EF,
在Rt△AOF中,OF=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∴FC=10-6=4,
设EC=x,则DE=EF=8-x,
在Rt△CEF中,EF2=EC2+FC2,
即(8-x)2=x2+42,
解得x=3,
∴EC的长为3,
∴DE=8-3=5,
又∵∠AFE=∠D=90°,
∴△AEF的面积=$\frac{1}{2}$×EF×AF=$\frac{1}{2}$×5×10=25.
故选:C.
点评 本题考查了矩形的性质、勾股定理的应用以及折叠的性质:折叠前后两图形全等,即对应线段相等,对应角相等;对应点的连线段被折痕垂直平分.解题时注意方程思想的运用.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:选择题
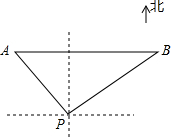 如图,小岛A位于港口P北偏西30°的方向,在小岛A的正东方向有一小岛B,小岛B位于港口P北偏东45°的方向,小岛A与港口P距离为20$\sqrt{3}$海里,则A,B两个小岛的距离为( )
如图,小岛A位于港口P北偏西30°的方向,在小岛A的正东方向有一小岛B,小岛B位于港口P北偏东45°的方向,小岛A与港口P距离为20$\sqrt{3}$海里,则A,B两个小岛的距离为( )| A. | 30海里 | B. | 30$\sqrt{3}$海里 | C. | 60海里 | D. | (30+10$\sqrt{3}$)海里 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
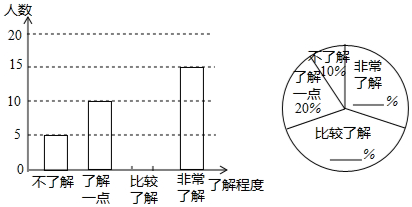
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
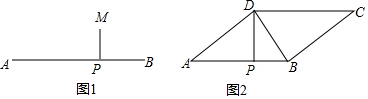
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com